Электрическое поле заряженной сферы.
Пусть сфера радиуса r0 несёт заряд q, равномерно распределённый по её поверхности с плотностью 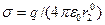 . Вследствие сферической симметрии в расположении зарядов в пространстве электрическое поле обладает такой же симметрией:
. Вследствие сферической симметрии в расположении зарядов в пространстве электрическое поле обладает такой же симметрией: 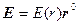 , где
, где 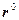 -единичный радиальный вектор сферической системы координат.
-единичный радиальный вектор сферической системы координат.
r
r0
S
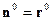
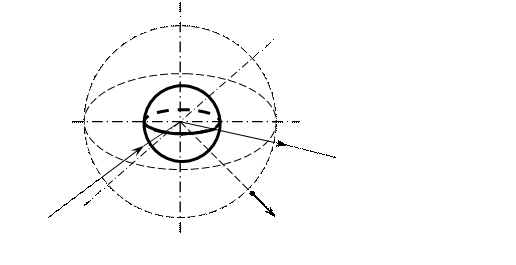
Рис.10. Заряженная сфера и воображаемая сферическая поверхность S
Построим воображаемую сферическую поверхность S радиуса r, окружающую заряженную сферу (рис. 10). Применим к этой поверхности электростатическую теорему Гаусса:
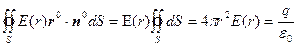
Здесь учтено, что на поверхности сферы S E(r)=const вследствие сферической симметрии электрического поля. Следовательно,
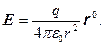
На наружной поверхности заряженной сферы
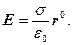
Если радиус поверхности S выбрать достаточно малым, чтобы она оказалась внутри заряженной сферы (r<r0), то заряд внутри поверхности S и электрический поток сквозь неё равны нулю. Значит, и напряжённость электрического поля внутри заряженной сферы равно нулю, как следует из соотношения 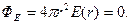
Электрический потенциал определим как напряжение между точкой с координатой r и точкой нулевого потенциала, находящейся на бесконечности:
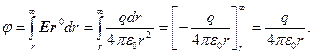
Потенциал самой сферы равен 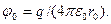
 2020-04-12
2020-04-12 163
163








