Изобразить переменную величину – это значит представить её аналитически (формулой) или графически (с помощью волновой или векторной диаграммы) таким образом, чтобы можно было определить её мгновенное значение.
Например, 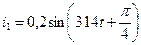
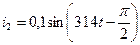 .
.
Для изображения переменной величины необходимо знать её параметры:
амплитуду или действующее значение;
частоту, или угловую частоту, или период;
начальную фазу.
В нашем примере 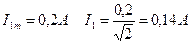
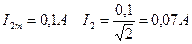 .
.

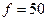 Гц Т = 0,02 с.
Гц Т = 0,02 с.
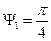
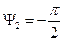 .
.
Подставляя t, можно определить мгновенные значения, например, t = 0,1 с
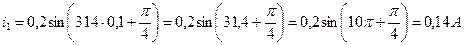 .
.
Графики зависимостей переменных величин от аргумента  называются волновыми диаграммами.
называются волновыми диаграммами.
 i 1, i 2 А
i 1 i 1, i 2 А
i 1
    0,2 0,2
   0,1 i 2
ωt 0,1 i 2
ωt
 –π/2 π/2 π 3/2 π 2π
–0,1
–0,2 –π/2 π/2 π 3/2 π 2π
–0,1
–0,2

| Ток i 1 первым достигает своей положительной амплитуды, ток i 1 опережает по фазе ток i 2. (i 2 отстаёт по фазе от i 1). |
| Если угол сдвига фаз 2-х переменных величин равен 0, то эти величины совпадают по фазе. |  e e
  e 1 e 1
 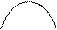 e 2
ωt e 2
ωt

|
Если 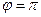 , то величины колеблются в противофазе. , то величины колеблются в противофазе.
|  e e
  e 1 e 1
   e 3 e 3
  ωt ωt

|
Переменную величину можно изобразить с помощью векторной диаграммы
Масштаб
 у 0,05A у 0,05A
  
ωt 1 i 1(t) I 1m
| Векторная диаграмма тока i 1 – это вектор, длина которого равна максимальному или действующему значению. В начальный момент времени вектор образует с осью х угол 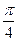 (угол, равный начальной фазе (угол, равный начальной фазе 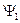 ), вектор вращается с угловой скоростью ), вектор вращается с угловой скоростью  против часовой стрелки. против часовой стрелки.
|
Мгновенное значение i 1 можно получить, проецируя вектор, занимающий в какой-то момент времени определённое положение на ось у, например, в момент t 1:
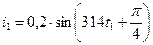
Векторная диаграмма для тока i 2:
0,05A

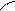


 ω
ω


 x
x
 –π/2
–π/2
I 2m
 2020-04-12
2020-04-12 92
92



 i 1(0) π/4
i 1(0) π/4 x
x






