Треугольники электрических величин

 

1. Треугольник напряжений

 

U          φ   U P = U L – U C                  U a

 

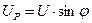
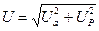
2. Треугольник сопротивлений (подобен треугольнику напряжений)

 

Z        φ  X = X L – X C       R

 

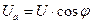
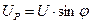
2. Треугольник мощностей (подобен треугольнику напряжений)

S                  Q = Q L – Q C       φ                P

P – активная мощность 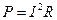Q – реактивная мощность 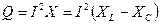S – полная мощность, единица измерения ВА

 

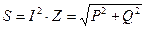
В случае 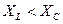           X < 0

                                          U _P< 0

                                                          Q < 0.

 

Резонанс напряжений

 

Резонанс напряжений – это физическое состояние цепи с последовательным соединением R, L, C при полной компенсации реактивных составляющих напряжения.

 

R   ~ u                                L                        C

Физическое условие резонанса U L = U C U P = 0 Рабочее условие резонанса X L = X C Учитывая, что X L = ωL, а 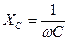ω 2 LC = 1

 

Установить в цепи режим резонанса можно изменением угловой частоты ω, индуктивности L или ёмкости С.

Частота при резонансе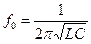

 

 

 

 

Волновая диаграмма                                          Векторная диаграмма

 

U L                         U a = U                                         I                                                φ = 0               U C

 

 

Особенности цепи при резонансе:

1. По отношению к генератору цепь ведёт себя как цепь с чистоактивным сопротивлением

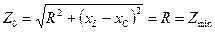
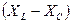                       = 0

 

Треугольник сопротивлений:               Z = R

2. Ток в момент резонанса достигает своего максимального значения

.

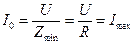3. Реактивная мощность при резонансе равна 0, т.е. нет обмена энергией между генератором и цепью.

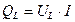
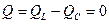
Полная мощность равна активной S = P.

 

 

Треугольник мощностей:                     S = P.

 

4. Если реактивные сопротивления больше активного, то напряжения на реактивных элементах превышают напряжение на зажимах цепи.

U _L и U _С > U _{а =} U _.

Это явление называется перенапряжением.

 

 

 

Резонансные кривые

 

Это графики зависимостей различных параметров цепи от частоты, или ёмкости, или индуктивности.

 

Параллельное соединение активного сопротивления, индуктивного и ёмкостного

 

i                   i а       i L        i C   ~ u       R      L            C

Пусть 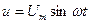по I закону Кирхгофа , где i a – активный ток 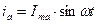, , где g – активная проводимость.

i _L – индуктивный ток

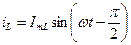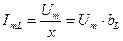, , где

b _L – индуктивная проводимость

i _С – ёмкостный ток

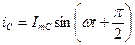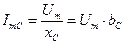, , где

b _С – ёмкостная проводимость

Единицы проводимостей – Сименс (См).

Реактивный ток i _P = i _L + i _C

Для векторов действующих значений:

 

                  – реактивный ток

Волновая диаграмма

                                                                             построена для случая b _C > b _L

                                            I _L > I _C

 

Векторная диаграмма

                          B

                          A

I C I P                         I P             φ  I a                                         U          I L

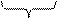I P Ток опережает напряжение на острый угол φ, т.е.цепь носит ёмкостный характер.

 

 

Закон Ома:

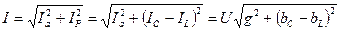
g – активная проводимость;

b _C – b _L = b – реактивная проводимость;

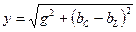– полная проводимость.

 

 

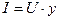
Это формула закона Ома для разветвлённой цепи.