1. Треугольник токов
I
I a
| 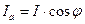
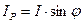
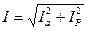
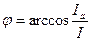
|
2. Треугольник проводимостей:
y
| 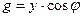
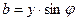
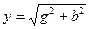
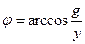
|
2. Треугольник мощностей (подобен треугольнику напряжений)
S
p | P – активная мощность
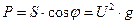 Q – реактивная мощность
Q – реактивная мощность
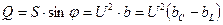 S – полная мощность
S – полная мощность
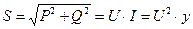
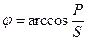
|
В случае 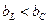 , цепь носит индуктивный характер;
, цепь носит индуктивный характер;
I P < 0
b < 0
Q < 0.
Резонанс токов
Резонанс токов – это физическое состояние цепи с параллельным соединением активного, индуктивного и ёмкостного элементов при полной компенсации реактивных составляющих тока.
i
      i a i L i C i a i L i C
| Физическое условие резонанса
I L = I C
Рабочее условие резонанса
b L = b C
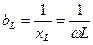
 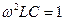
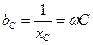
| |||||||||||
Установить в электрической цепи режим резонанса можно изменением частоты ω, индуктивности L или ёмкости С.
Частота при резонансе 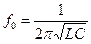
Волновая диаграмма
u, i a, i L, i C
–π/2 π/2 π 3/2π 2π ωt
| Векторная диаграмма
 I C
I a = I I C
I a = I
U φ = 0
I L
|
Особенности цепи при резонансе
1. По отношению к генератору цепь выступает как цепь с чистоактивной проводимостью
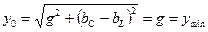
Это наименьшее значение проводимости.
Треугольник проводимостей g = y b = 0.
2. В момент резонанса ток достигает минимального значения

3. Реактивная мощность при резонансе равна 0.
Q = Q C – Q L = 0, т.к. Q C = U·I C = Q 2 = U · I L
Полная мощность равна активной.
Треугольник мощностей P = S Q = 0.
4. Если реактивные проводимости b L и b C больше активной g, то токи, проходящие через реактивные элементы, превышают ток в неразветвлённой части цепи.
Если b L> g, то I L и I С > I a = I.
Резонансные кривые
Это графики зависимости различных параметров цепи от частоты, или от ёмкости, или от индуктивности.



 I, I a, I L, I C, φ
I, I a, I L, I C, φ
 |
 I C
I C
I

 I a
I a
 I L
I L


 ω
ω
ω0 φ
 |
 XC<XL XC>XL – ёмкостный характер цепи
XC<XL XC>XL – ёмкостный характер цепи
индуктивный характер цепи
Параллельное соединение реальной катушки и конденсатора с потерями
i

   i 1 i 2 i 1 i 2
R1 R2
| Для расчёта такой цепи используют метод проводимостей, согласно которому последовательное соединение элементов заменяют эквивалентным параллельным. |
1 ветвь:

 i 1
R1 i 1
R1
  ~ u
L1 ~ u
L1
|
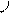      I 1a U I 1a U
 I 1L I 1 I 1L I 1
 Раскладываем
Раскладываем 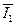 на два перпендикулярных направления.
Последовательное соединение заменяем параллельным. на два перпендикулярных направления.
Последовательное соединение заменяем параллельным.
|
g 1 b L1
| I 1a = Ug 1
I 1L = U·b L1
Определим параметры g 1 и b L1 эквивалентной схемы.
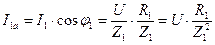 ,
с другой стороны I 1a = Ug 1 ,
с другой стороны I 1a = Ug 1
| ||||||||||||||||||||



 Следовательно, для того, чтобы замена была эквивалентной, активная проводимость 1-й ветви
Следовательно, для того, чтобы замена была эквивалентной, активная проводимость 1-й ветви 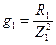
где Z 1 – полное сопротивление первой ветви 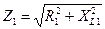 .
.
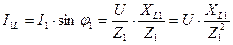 ,
,
С другой стороны 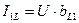 .
.
Следовательно, при эквивалентной замене индуктивная проводимость 1-й ветви 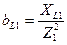 .
.
Аналогичные рассуждения можно сделать для 2-й ветви электрической цепи и заменить последовательное соединение
   i 1 i 1
R2
| эквивалентным параллельным |
|

|
в которой
g 2 – активная проводимость 2-й ветви
R2 – активное сопротивление
Z2 – полное сопротивление 2-й ветви. 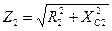 .
.
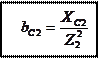 |
 – ёмкостная проводимость 2-й ветви;
– ёмкостная проводимость 2-й ветви;
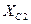 – ёмкостное сопротивление;
– ёмкостное сопротивление;
Z2 – полное сопротивление 2-й ветви 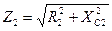 .
.
Единица измерений проводимостей – Сименс (Си).
Таким образом, вычислив параметры, мы получили эквивалентную схему:
 i i
     i 1 i 2 i 1 i 2
| Определить составляющие тока можно по формулам:
I 1a = Ug 1 I 2a = Ug 2
I 1L = U·b L1 I 2С = U·b С2
Токи ветвей:
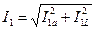
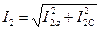
| ||||||||||||||||||||||||||||||||||||||||
Векторная диаграмма
     I 2C I 2 I 2C I 2
    I 2a I 2a
    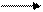 I 1a I a U I 1a I a U
  I P I I P I
 I 2c
I 2c
 I 1L I 1 I 1L I 1
| I a = I 1a + I 2a
I P = I 2C – I 1L
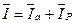 По модулю:
По модулю:
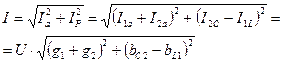
|
Порядок построения векторной диаграммы:
1. 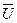
2. 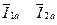
3. 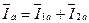
4. 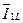
5. 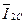
6. I P = I 2C – I 1L
7. 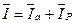
8. 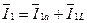
9. 
Литература
1. Лоторейчук Е.А. Теоретические основы электротехники. М. Форум, Инфра–М, 2006.
2. Евдокимов Ф.Е. Теоретические основы электротехники. М. изд. Центр «Академия», 2004.
 2020-04-12
2020-04-12 140
140


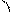 φ I P
φ I P
 g
g










 u i p = 0
u i p = 0


 0
0




 L1 C2
L1 C2




 i 1а i 1L
i 1а i 1L





 С2
С2

 i 2
i 2


 g 2 b C2
g 2 b C2

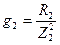







 ~u g 1 b L1 g 2 b С2
~u g 1 b L1 g 2 b С2







