Основні теореми диференціального числення.
Теорема Ферма: Нехай функція f(х) неперервна на інтервалі 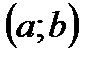 і набуває свого найбільшого або найменшого значення у деякій точці с цього інтервалу. Тоді, якщо в точці с існує похідна
і набуває свого найбільшого або найменшого значення у деякій точці с цього інтервалу. Тоді, якщо в точці с існує похідна  то
то 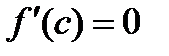 .
.
Доведення: Для визначеності вважатимемо, що в точці с функція  набуває свого найбільшого значення, тобто
набуває свого найбільшого значення, тобто  (3)
(3)
Оскільки точка с є внутрішньою точкою інтервалу  , то приріст
, то приріст  може бути як додатним, так і від’ємним, а відповідний приріст функції, як випливає з умови (3), не може бути додатним:
може бути як додатним, так і від’ємним, а відповідний приріст функції, як випливає з умови (3), не може бути додатним: 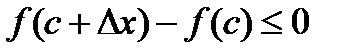 . Звідси при
. Звідси при  маємо
маємо  , тому
, тому  . Аналогічно, якщо
. Аналогічно, якщо 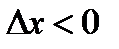 , то
, то  . За умовою похідна існує, тобто
. За умовою похідна існує, тобто 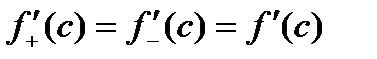 . Тоді за умов
. Тоді за умов  випливає, що
випливає, що  . Теорему доведено.
. Теорему доведено.
Геометричний зміст теореми Ферма зрозумілий з малюнка: якщо в точці  функція
функція  досягла найбільшого чи найменшого значення, то дотична до графіка цієї функції в точці
досягла найбільшого чи найменшого значення, то дотична до графіка цієї функції в точці 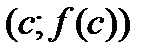 паралельна осі
паралельна осі  .
.
Теорема Ролля: Якщо функція f(х) неперервна на відрізку  , диференційована в інтервалі
, диференційована в інтервалі  і на кінцях відрізка набуває однакових значень
і на кінцях відрізка набуває однакових значень  , то знайдеться хоча б одна точка
, то знайдеться хоча б одна точка 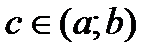 , в якій
, в якій  .
.
Доведення: Оскільки функція f(х) неперервна на відрізку  , то вона досягає на цьому відрізку свого найбільшого значення
, то вона досягає на цьому відрізку свого найбільшого значення 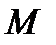 і найменшого значення
і найменшого значення  . Якщо
. Якщо  , то
, то  і
і 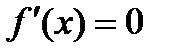 в довільній точці
в довільній точці 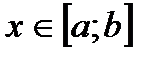 .
.
Нехай 
Тоді хоча б одне із значень  чи
чи 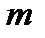 досягається функцією у внутрішній точці інтервалу
досягається функцією у внутрішній точці інтервалу  , тому що
, тому що 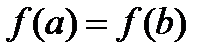 . За теоремою Ферма похідна в такій точці дорівнює нулю. Теорему доведено.
. За теоремою Ферма похідна в такій точці дорівнює нулю. Теорему доведено.
Геометричний зміст теореми Ролля: якщо функція задовольняє умови теореми Ролля, то на графіку цієї функції знайдеться хоча б одна точка, в якій дотична паралельна осі  .
.
Теорема Коші: Якщо функції  і
і  неперервні на відрізку
неперервні на відрізку 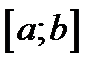 , диференційовні в інтервалі
, диференційовні в інтервалі  , причому
, причому  , то існує така точка
, то існує така точка  , що
, що
 .
.
Доведення: Введемо допоміжну функцію
 , яку можна розглядати на відрізку
, яку можна розглядати на відрізку 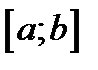 , бо
, бо  . У противному разі за теоремою Ролля знайшлася б точка
. У противному разі за теоремою Ролля знайшлася б точка  , в якій
, в якій  , що неможливо, бо за умовою
, що неможливо, бо за умовою  . Неважко пересвідчитись, що функція
. Неважко пересвідчитись, що функція 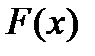 задовольняє всі умови теореми Ролля. Тому знайдеться точка
задовольняє всі умови теореми Ролля. Тому знайдеться точка  , в якій
, в якій  або
або
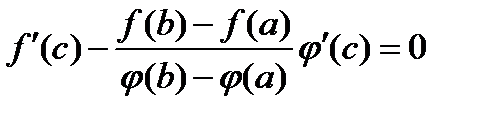 ,
,
звідки й випливає формула  . Теорему доведено.
. Теорему доведено.
Теорема Лагранжа: Якщо функція  , неперервна на відрізку
, неперервна на відрізку  , диференційовна в інтервалі
, диференційовна в інтервалі  , то всередині цього інтервалу знайдеться хоча б одна точка
, то всередині цього інтервалу знайдеться хоча б одна точка  , в якій
, в якій 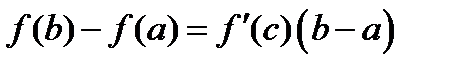 .
.
Доведення: Цю теорему можна розглядати як окремий випадок теоремиКоші. Справді, поклавши у формулі 
 , дістанемо формулу
, дістанемо формулу 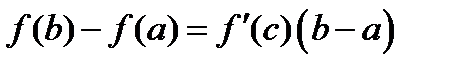 . Теорему доведено.
. Теорему доведено.
Розглянемо геометричний зміст теореми Лагранжа
Запишемо формулу 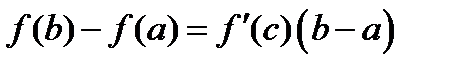 у вигляді
у вигляді
 ,
,
тоді  .
.
Тобто якщо функція  задовольняє умови теореми Лагранжа, то на графіку цієї функції знайдеться хоча б одна точка, в якій дотична до графіка паралельна хорді, що сполучає кінці кривої
задовольняє умови теореми Лагранжа, то на графіку цієї функції знайдеться хоча б одна точка, в якій дотична до графіка паралельна хорді, що сполучає кінці кривої  і
і  . Таких точок може бути і кілька, але хоча б одна завжди існує.
. Таких точок може бути і кілька, але хоча б одна завжди існує.
 2020-04-12
2020-04-12 113
113








