Системи лінійних рівнянь: метод Крамера,метод Гауса,метод оберненої матриці

Означення: Системою т лінійних рівнянь з п невідомими 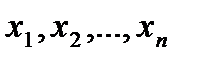називається система виду

.        (1)

Числа , і=1,2,...,т; j=1,2,...,п біля невідомих називаються коефіцієнтами, а числа - вільними членами системи (1).

Означення: Система рівнянь (1) називається однорідною, якщо всі вільні члени дорівнюють нулю, і неоднорідною, якщо хоч один з них відмінний від нуля.

Означення: Упорядкований набір п чисел ( 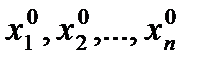) називається розв’язком системи (1), якщо при підстановці цих чисел замість невідомих 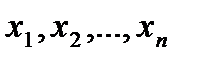усі рівняння системи перетворюються в тотожності.

Означення: Система рівнянь (1) називається сумісною, якщо вона має хоча б один розв’язок, і несумісною, якщо вона не має жодного розв’язку.

Означення: Сумісна система називається визначеною, якщо вона має єдиний розв’язок, і невизначеною, якщо вона має більш ніж один розв’язок.

Означення: Дві системи лінійних рівнянь називаються еквівалентними, якщо вони мають одну й ту ж множину розв’язків.

Еквівалентні системи дістають, зокрема, внаслідок елементарних перетворень даної системи. Елементарні перетворення системи лінійних рівнянь відповідають елементарним перетворенням матриці за умови, що вони виконуються лише над рядками матриці.

Розглянемо способи розв’язування системи лінійних рівнянь, у якої кількість рівнянь співпадає з кількістю невідомих, тобто систему

  (2).                        

Визначник

           (3)

називається визначником системи (2).

Введемо в розгляд визначники

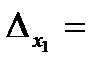
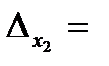
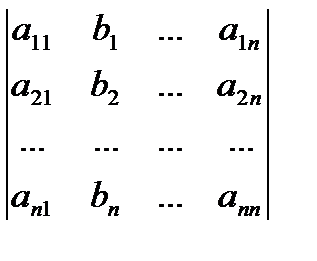; ;...; ,   (4)

Визначники (4) утворені з визначника (3) заміною відповідних стовпців стовпцем вільних членів системи (2).

Теорема 3: Якщо визначник системи (2) відмінний від нуля, то система сумісна і має розв’язок, що визначається за формулами

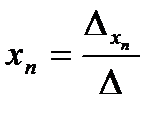,  ,..., , (5)

в яких числа є визначниками (4).

Доведення: Доведемо дану теорему для системи двох лінійних рівнянь з двома невідомими х і у:

(6)

Виконаємо такі елементарні перетворення системи (6): спочатку помножимо перше рівняння на 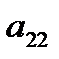, друге на , а потім додамо їх; після цього перше рівняння помножимо на , а друге – на і додамо їх. Дістанемо систему

       (7)

Систему (7) можна записати за допомогою визначників:

       (8)

де - головний визначник системи, , . Тоді

Теорему доведено.

При розв’язуванні рівнянь (8) можуть бути такі випадки:

1) , тоді система (6) має єдиний розв’язок:

,   .

2) або , тоді система не має розв’язків, тобто є несумісною.

3) , тоді система зводиться до одного рівняння і має безліч розв’язків, тобто є невизначеною.

Ці ж випадки виконуються і для систем лінійних рівнянь з багатьма змінними.

Розглянемо як розв’язується система лінійних рівнянь методом оберненої матриці.

Введемо в розгляд матриці:

; ; .

Матрицю А, складену з коефіцієнтів системи (2), називають матрицею або основною матрицею системи, матрицю Х – матрицею з невідомих, а матрицю В – матрицею з вільних членів. Тоді згідно з правило множення матриць систему (2) можна записати одним матричним рівнянням з невідомою матрицею Х:

   (9)

Припустимо, що матриця А системи (2) має обернену матрицю 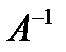; помножимо обидві частини рівності (9) на зліва:

(10)

Отже, щоб розв’язати систему рівнянь (2), достатньо знайти матрицю, обернену до матриці системи, і помножити її зліва на матрицю з вільних членів.

Формулу (10) називають матричним записом розв’язку системи (2) або розв’язком матричного рівняння (9).

12. Існує ще один спосіб розв’язування системи лінійних рівнянь – метод Гаусса, який інакше ще називають методом послідовного виключення невідомих. Даний метод ґрунтується на елементарних перетвореннях системи лінійних рівнянь. Розглядається система рівнянь (1), яка зводиться до трапецієвидної форми виду:

     (11)

Дослідимо цю систему:

1. Якщо система містить рівняння виду і , то вона очевидно несумісна.

2. Нехай система (11) не містить рівнянь виду ( ). Назвемо невідомі основними, а всі інші, якщо вони є вільними. Основних невідомих за означенням 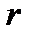. Надаючи вільним невідомим довільні значення і підставляючи ці значення в рівняння системи, з 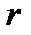- го рівняння знайдемо . Підставивши це значення в перші рівняння і, піднімаючись вгору по системі, знайдемо всі основні невідомі. Оскільки вільні невідомі можуть набувати будь-яких значень, то система має безліч розв’язків.

3. Нехай в системі (11) . Тоді вільних невідомих немає, тобто всі невідомі основні і система має так званий трикутний вигляд:

З останнього рівняння знайдемо і, піднявшись по системі вгору, знайдемо всі інші невідомі. Отже, в цьому випадку система має єдиний розв’язок.

 

 

14.Класична постановка задач лінійного програмування.

Задачі на знаходження найбільшого чи найменшого значень деякої функції є типовими прикладами задач лінійного програмування. Функцію, найбільше або найменше значення якої вимагається знайти називають цільовою функцією. У задачах лінійного програмування цільова функція є лінійною функцією двох змінних.

З економічної точки зору задачі лінійного програмування пов’язані з пошуком способів найкращого розподілу і використання обмежених ресурсів (робоча сила, сировина, матеріали, засоби виробництва). При цьому шукають такий план (програму), який при певних обмеженнях на ресурси дає змогу досягнути, наприклад, найбільшого випуску продукції, найменших витрат виробництва тощо.

У загальному вигляді задачу лінійного програмування можна записати так: знайти максимальне або мінімальне значення функції

при заданій системі обмежень

,

– деякі числа, 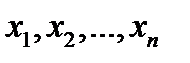– змінні. Слід сказати, що у системі знаки нерівності можуть бути строгими, а можуть бути замінені знаками рівності.

Типовими задачами лінійного програмування є задача про використання ресурсів, задача раціонального харчування і транспортна задача.

Задача про використання ресурсів або інакше задача про максимальну рентабельність підприємства: як використати запаси сировини, що є на підприємстві, для виготовлення тієї чи іншої продукції, щоб дохід підприємства був найбільшим?

Приклад 3. Скласти математичну модель задачі лінійного програмування – задачі отримання максимального прибутку фірми: підприємство випускає продукцію двох видів А і Б. види сировини, їх запаси, норми витрат сировини на умовну одиницю продукції кожного виду занесені в таблицю:

Вид сировини	Запаси сировини	Норма витрат сировини на одиницю продукції кожного виду
		А	Б
І	450	2	3
ІІ	180	1	4
ІІІ	240	4	2

 

Дохід виробництва від реалізації умовної одиниці продукції виду А дорівнює 5 грн., а виду Б – 8 грн. Спланувати так випуск продукції, щоб дохід підприємства був найбільшим.

Розв’язування:

Позначимо через – кількість продукції виду А, – кількість продукції виду Б. Користуючись даними таблиці, складаємо систе6му обмежень:

Цільова функція матиме вигляд: .

Задача раціонального харчування полягає в наступному: із наявних продуктів потрібно скласти таку дієту, яка задовольняла б потреби людини в поживних речовинах (жирах, білках, вуглеводах, вітамінах і т.д.) і вимагала б найменших затрат.

Транспортна задача полягає в організації перевезення вантажів з одних пунктів в інші так, щоб загальна вартість перевезень була мінімальною. Як і якими способами розв’язуються дані задачі буде розглянуто в наступній лекції.

 

15. Системи лінійних нерівностей, їх розвיязування графічним способом.

1. Означення: Нерівність виду або називається лінійною нерівністю з двома змінними величинами і ( – дійсні числа).

Точки ( ),які задовольняють рівняння лежать на прямій, яка ділить площину на дві півплощини.

Означення: Множина точок площини, які лежать по один бік від прямої і не лежать на цій прямій називається відкритою півплощиною.

Означення: Множина точок площини, які лежать по один бік ввід прямої разом з точками цієї прямої називається замкненою півплощиною

Теорема: Усі точки однієї з двох відкритих півплощин, на які пряма поділяє площину задовольняють нерівність , а всі точки іншої відкритої півплощини нерівність .

Для того, щоб з’ясувати, в якій півплощині виконується нерівність , досить обчислити вираз для точки , що не лежить на прямій. Якщо пряма не проходить через початок координат, то за точку М зручно брати початок координат.

Приклад 1. Розв’язати графічно нерівність: .

Розв’язання:

Розглянемо рівняння прямої і побудуємо її:

Перевіримо, якій з півплощин належить точка , яка задовольняє нашу нерівність. Півплощина, якій належить точка М і буде розв’язком нашої нерівності.

Означення: Система нерівностей виду

(1)

де 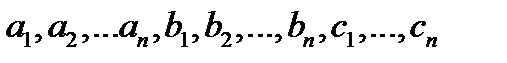– дійсні числа, називається системою нерівностей з двома змінними.

Система (1) називається сумісною (несуперечливою), якщо існує хоча б одна точка для якої виконуються всі нерівності системи.

Кожна з нерівностей системи (1) виконується лише для точок із замкненої півплощини, на які ділить півплощину пряма .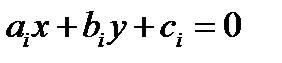

Означення: Непустий перетин деякої кількості замкнутих півплощин називається замкненим многокутником.

Означення: Непустий перетин деякої кількості відкритих півплощин називається відкритим многокутником.

Користуючись цими означеннями, основний результат про розв’язування системи нерівностей можна сформулювати так:

Розв’язком сумісної системи нерівностей (1), тобто множиною всіх точок , для яких виконуються всі нерівності системи є замкнений многокутник. І навпаки кожний замкнений многокутник є розв’язком системи нерівностей типу (1).

Приклад 2. Розв’язати систему нерівностей:

Розв’язання:

Побудуємо прямі . За допомогою вибраних навмання точок, перевіряємо яка з півплощин є розв’язком для кожної нерівності. Одержуємо розв’язок системи:

 

 

16. Графічний метод розвיязування задач лінійного програмування.

Управління господарською діяльністю починається з планування – вибору єдиного плану з множини різних варіантів. Найкращий план називається оптимальним.

 

    Множина можливих варіантів, серед яких вибирається оптимальний план завжди обмежена (ресурсами сировини, наявністю робочої сили, кількістю обладнання, транспорту і т.д.). Кожен з варіантів розв’язку може бути допустимим, якщо він задовольняє існуючі обмеження. Задача знаходження оптимального плану зводиться до математичної задачі – задачі знаходження найбільшого чи найменшого значень функції при заданих обмеженнях.

 

    Ми вже вияснили, що кожне обмеження з геометричної точки зору являє собою відкриту або замкнену півплощину, а перетин таких півплощин утворює деякий опуклий многокутник Ω.. Свого найбільшого або найменшого значення цільова функція досягне у одній з вершин многокутника. Але інколи вершин многокутника може бути дуже багато. І перебирання допустимих розв’язків займе певний час. Тому доцільно скористатись поняттями ліній рівня і вектора найбільшого зростання цільової функції. В загальному випадку задача лінійного програмування має вигляд:

 

f (x1, x2,..., xn) = c1 x1 + c2 x2 +... + cn xn → min (max)

 

 

    Якщо ми розглянемо випадок n = 2, то f (x1; x2) = c1 x1 + c2 x2.

 

    Графіком функції с1х1+с2х2=с є пряма. При різних значеннях одержимо різні прямі, які називаються лініями рівня цільової функції. Паралельним перенесенням цих ліній в одному напрямку ми одержимо зростання цільової функції, в іншому – її спадання. Напрям збільшення значень функції, який перпендикулярний до ліній рівня, називається напрямом найбільшого зростання цільової функції. Цей напрям отримаємо, коли відкладемо від початку координат вектор n, що має координати n = (c1; c2), де с1, с2 – коефіцієнти цільової функції. Серед всіх ліній рівня вибираємо дві крайні лінії, які вказують на вершини многокутника, де функція досягає свого найбільшого та найменшого значень. Отже, графічний спосіб розв’язання задачі лінійного програмування полягає у:

 

1) побудові многокутника Ω;

 

2) побудові вектора n;

 

3) підстановці в функцію крайніх (по напряму вектора) точок.

 

Недоліки графічного способу:

 

а) його застосовують лише у випадку двох змінних;

 

б) громіздкість.

 

 

17.Розвיязування задач лінійного програмування симплекс-методом.

Алгебраїчний спосіб розв’язування задачі лінійного програмування – це симплекс-метод.

   Симплекс-метод якраз і дає можливість знайти спочатку будь-яку вершину многокутника Ω, а потім від неї перейти до тієї, в якій значення функції z не менше, ніж у попередній.

   В симплексному методі можна виділити наступні етапи розв’язку:

- перетворення обмежень – нерівностей в рівності;

- вибір першого допустимого плану;

- перевірка оптимальності плану;

- перепланування (перетворення симплекс-таблиць).

Охарактеризуємо кожний етап:

Перетворення обмежень-нерівностей в рівності здійснюють шляхом введення нових змінних, які треба додати до лівої частини, щоб нерівності перетворились в рівності. Всі невідомі в задачах лінійні програмування можуть приймати тільки додатні чи нульові значення (вихідні дані х невідיємні по змісту економічних задач, а додаткові змінні по накладених умовах).

Основне правило розв’язку симплекс-метод передбачає поділ всіх змінних на основні (додатні) і неосновні (нульові). Кожний наступний поділ змінних на основні і неосновні змінні геометрично означає, що в якості нового допустимого плану розглядається одна з сусідніх вершин многокутника. Розглянуті перетворення системи обмежень з перебором різних варіантів здійснюють у вигляді перетворення таблиць. Кожна наступна симплексна таблиця відображає наступний допустимий план.

Правило перевірки оптимальності розв’язку заключається в перевірці знаків елементів останнього рядка: якщо всі вони від’ємні, то план оптимальний, якщо ні, то слід здійснити перепланування.

Для проведення перепланування слід вибрати ключовий рядок і ключовий стовпець.

Правило вибору ключового стовпця: за ключовий беремо стовпчик з найбільшим додатним елементом в цільовому рядку.

Правило вибору ключового рядка: знаходимо найменше за модулем відношення вільних членів до відповідних елементів ключового стовпця.

На перетині ключового стовпця і ключового рядка стоїть ключовий елемент.

За вибраним таким чином ключовим елементом виконуємо крок Жорданового виключення. Якщо ключовий елемент відмінний від 1, то ділимо ключовий рядок на ключовий елемент.

Процес повторюється до знаходження оптимального плану.

Приклад. Розв’язати задачу лінійного програмування симплекс-методом.

 

Розв’язування:

базис	Х	A1	A2	A3	A4	A5
A3	18	2	3	1	0	0
A4	35	5	7	0	1	0
A5	15	3	5	0	0	1
z	0	7	5	0	0	0
A3	8	0	-1/3	1	0	-2/3
A4	10	0	-4/3	0	1	-5/3
A1	5	1	5/3	0	0	1/3
z	-35	0	-20/3	0	0	-7/3

 

 

 

18.Транспортна задача і методи її розвיязування.

Серед задач лінійного програмування особливе місце займає транспортна задача. Це обумовлено, по-перше, практичним значенням транспортної задачі, по-друге, транспортна задача має такі специфічні особливості, які дозволяють суттєво спростити загальні методи розв’язування. Формулюється транспортна задача так:

Є постачальників однорідної продукції. Максимальні об’єми поставок продукції задані і рівні . Ця продукція використовується споживачами 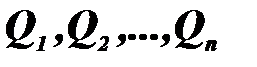. Об’єми споживання задані і рівні . Вартість перевезення одиниці продукції від і-го постачальника до j-го споживача відома для і дорівнює . Ставиться задача – встановити такі об’єми перевезень від кожного постачальника до кожного споживача , щоб сумарні затрати на перевезення були мінімальними і потреби всіх споживачів були задоволені (якщо це можливо). Математична модель задачі має вигляд:

Якщо виконується умова , то транспортна задача буде закритою.

При розв’язуванні транспортної задачі базисні розв’язки (вершини многокутника) грають особливу роль. Невироджений базисний розв’язок транспортної задачі містить рівно ненульових перевезень . В іншому випадку базисний розв’язок містить менше ніж перевезень. Дані транспортної задачі і обчислення заносяться в транспортну таблицю. Від звичайної симплекс-таблиці вона відрізняється тим, що в ній заповнені тільки ті клітинки, де перевезення ненульові. Вихідна транспортна таблиця має вигляд:

	Q1	Q2	…	Qn	ai
P1	c11	c12	…	c1n	a1
P2	c21	c22	…	c2n	a2
…	…	…	…	…	…
Pm	cm1	cm2	…	cmn	am
bj	b1	b2	…	bn

 

Методи розв’язування транспортної задачі:

1. Метод північно-західного кута.

Даний метод полягає в тому, що транспортну таблицю заповнюють ненульовими перевезеннями, починаючи з верхньої лівої (північно-західної) клітинки. При цьому розподіляють продукцію першого постачальника, максимально задовольняючи першого споживача, потім другого і т.д. до повного розподілу продукції першого постачальника. Потім розподіляють продукцію другого постачальника, причому якщо в деякому пункті Q_j потреби не були задоволені, то поставки будуть здійснюватись і від другого постачальника. І так далі. Сума перевезень в і-му рядку рівна a_i, в j-му стовпці – b_j. Одержаний таким чином план перевезень буде допустимим розв’язком транспортної задачі.

2. Метод мінімального елемента.

Ідея методу полягає в тому, щоб максимально загрузити перевезеннями комунікації з мінімальними транспортними витратами. Тут таблицю будемо заповнювати, починаючи з “дешевих” кліток. Метод реалізується наступним чином: на першому кроці визначаємо мінімальний елемент матриці С. Нехай це буде . Покладемо . Можливі два випадки:

1) (можливості постачальника менші потреб споживача). Тоді нулями заповнюється 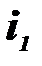-рядок, крім елемента 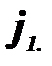Далі в обчисленнях не використовується.

2) (можливості постачальника більші потреб споживача). Тоді нулями заповнюється -стовпець, крім елемента Далі не використовується споживач .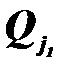

На другому кроці з матриці викреслюється відповідний рядок чи стовпець. Одержуємо матрицю . Вважаємо, що

Другий крок – це виконання описаних операцій з матрицею Продовжуємо до повного заповнення транспортної таблиці або викреслювання рядків чи стовпців матриці

 

19.Метод потенціалів – як один з методів розвיязування транспортної задачі.

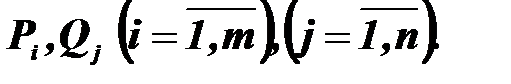Нехай потенціали пунктів Назвемо величину відносною оцінкою змінної Тоді базисний розв’язок оптимальний тоді і тільки тоді, коли існують потенціали , такі, що відносні оцінки для базисних (зайнятих) кліток транспортної таблиці і для не базисних (вільних) кліток. Суть методу потенціалів полягає в наступному:

1. В якості першого наближення до оптимального розв’язку береться довільний початковий базисний розв’язок (побудований будь-яким іншим методом).

2. Визначаються потенціали , так, щоб в кожній базисній клітці виконувалась умова або Відмітимо, що така система містить -1 рівняння (по кількості базисних кліток) і невідомих. Тому одну із змінних задають довільно (наприклад ), інші знаходять з вказаної системи.

3. Обчислюються відносні оцінки для не базисних (вільних кліток). Якщо для всіх цих кліток , то перевірений базисний розв’язок оптимальний. Якщо ж для всіх цих кліток , то досліджуваний базисний розв’язок можна покращити, вводячи в число базисних одну із вказаних кліток (зазвичай ту, для якої відносна оцінка мінімальна). Нехай це ( ). Розглянемо питання про те, яка із базисних кліток виводиться із числа базису. Із кліток транспортної таблиці створюємо цикл (замкнутий ланцюжок) так, щоб він містив не базисну клітку, а інші клітки були базисними. Він може бути у вигляді прямокутника, квадрата, многокутника:

 

        Помітимо клітки циклу наступним чином: небазисну знаком “+”, інші знаком “+” чи “-”, але так, щоб сусідні по рядку чи по стовпцю клітинки мали різні знаки. Збільшуємо тепер об’єм перевезень, що знаходяться в клітинках з знаком “+” на величину , а об’єм перевезень, що стоять в клітинках з знаком “-” зменшимо на ту ж величину. Очевидно, якщо в якості вибрати мінімум серед від’ємних кліток, то в результаті такого перерозподілу вантажу одна із базисних кліток стане вільною, а клітка ( ) увійде в базис.

4. За допомогою описаної процедури перерозподілу вантажів по циклу, одержимо новий базисний розв’язок, який треба перевірити на оптимальність. Процес повторюється і т. д. аж поки для певного базисного розв’язку не буде виконаний критерій оптимальності.

В не виродженому випадку метод потенціалів приводить до оптимального розв’язку за скінчену кількість кроків. У виродженому випадку, якщо зайнятих клітинок менше ніж , можливе за циклювання, для попередження якого необхідні додаткові міри.

 

20.Похідна. Звיязок диференційовності і неперервності функції.

   Означення. Похідною функціїу = f (х) в точці х називається границя відношення приросту функції Δу в цій точці до приросту аргументу 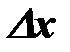, коли приріст аргументу прямує до нуля.

Таким чином, за означенням

.

   Якщо в деякій точці x границя , то похідну f′ (х) в цій точціназивають нескінченною.

   Якщо в деякій точці x границя не існує, то не існує в цій точці і похідної.

   Значення похідної функції 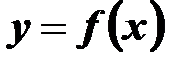в точці позначається одним із таких символів: .

З означення похідної випливає такий спосіб її знаходження:

1) надати значенню х довільного приросту 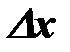і знайти відповідний приріст функції ;

2) знайти відношення ;

3) знайти границю цього відношення: .

Якщо ця границя існує, то вона й дорівнює похідній .

 Теорема. Якщо функція у = f(x) диференційована в деякій точці хп, то вона в цій точці неперервна.

Доведення. Якщо у = f(x) диференційована в точці х0, то згідно

з означенням похідної при х = хп існує скінченна границя

lim —^ = / (хп).

^Ах °

В силу того, що границя змінної величини відрізняється від самої змінної лише на нескінченно малу a, то з останньої рівності маємо

= / (xn) + a=>Ду = / (xn)Ax + am;. (7)

Оскільки / (х0) - постійна величина, то з властивостей не-скінченно малих випливає, що обидва доданки в правій частині (7) є нескінченно малих величинами. їз (7) випливає, що Ьу —> 0, тоб-

то функція у = f(x) неперервна в точці х0. Теорема доведена.

▼ Наслідок. 3 ціег теореми випливае, що неперервність функціг е необхідною умовою диференційованості функціг. Це означае, що в точ-ках розриву функція не мае похіднш, тобто вона не диференційована.

Функція, яка неперервна в точці хп, може бути не диференційо-

ваною в цій точці. Наприклад, функція у = \х\ неперервна в точці

X = 0, але не має похідної в цій точці тому, що

lim — = -1, a lim —^ = 1,

Ґ Ау ґ

тоото границя відношення^ залежить від спосооу прямуван-

Ах ня Ах —> 0. Частина 8. Диференціальне числення функцій однієї змінної

+1