2020-04-12
123
Нехай 
- неперервна на 
функція. Позначимо через 
- будь-який набір точок з , що 
. Набір Т – розбиття на 
частин.
Розглянемо 
– довжина 
. Для кожного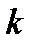 
визначимо числа 
– найменше і найбільше значення функції на : 
, 
.
Означення. Нижньою сумою Дарбу для функції і набору точок Т на називається сума 
:
.
Означення: Верхньою сумою Дарбу для функції і набору точок Т на називається сума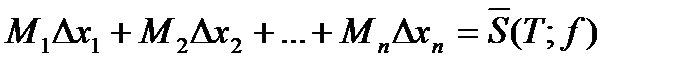 
.
Очевидно, що 
Геометрична інтерпретація:
Якщо на кожному з проміжків вибрати точку 
: 
і знайти суму добутків 
, то позначивши 
, цю суму називають інтегральною сумою для функції 
і розбиття Т.
Геометрична інтерпретація:Зрозуміло, що 
.
Суми Дарбу – нижня і верхня інтегральні суми.
Означення. Якщо існує єдине число І таке, що для будь-якого набору справджується рівність 
, то число І називається визначеним інтегралом від функції на :
, 
- межі інтегрування.
Геометричний зміст визначеного інтеграла:
Інтеграл дорівнює площі криволінійної трапеції, яка обмежена віссю 
, прямими 
, 
і графіком функції :
|
|
|
Умови інтегрованості функції.
Теорема 1. (необхідна умова). Якщо функція неперервна на , то вона інтегрована на цьому відрізку.
Теорема 2. (достатня умова). Якщо функція неперервна на , то вона інтегрована на цьому відрізку.
Теорема 3. Якщо функція обмежена на і неперервна в ньому скрізь, крім скінченого числа точок, то вона інтегрована на цьому відрізку.
