Первісна , невизначений інтеграл та його властивості

Нехай задано функцію f, визначену на скінченому або нескінченному проміжку, і треба знайти функцію F, похідна від якої у будь-якої дорівнює f: 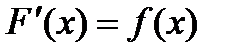для всіх або .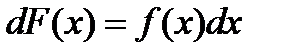

Означення: Функція 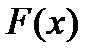, визначена на ,похідна від якої цьому проміжку дорівнює даній функції , називається первісною для функції або для диференціала .

Зрозуміло, що функція теж буде первісною для функції на :

Теорема: Якщо функція 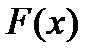є якою-небудь первісною для функції на , то множина всіх первісних для функції на цьому проміжку міститься у формулі .

Доведення: Функція 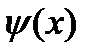- первісна для (було показано раніше).

Припустимо, що 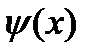– будь-яка первісна для на . Тоді , .

Тоді 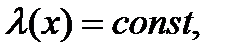. Теорему доведено.

Якщо 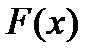- первісна для на і , то вираз називається невизначеним інтегралом функції і позначається символом

Функція називається підінтегральною функцією, вираз називається підінтегральним виразом, а знак ∫ називається інтегралом, тобто

З геометричної точки зору, невизначений інтеграл є множиною кривих, кожна з яких називається інтегральною кривою і утворюється зсувом (паралельних перенесень)однієї з них паралельно самій собі уздовж осі.

Властивості невизначеного інтеграла

1. Похідна від невизначеного інтеграла дорівнює підінтегральній функції: .

Доведення: .

2. Невизначений інтеграл від диференціала деякої функції дорівнює сумі цієї функції і довільної сталої:

Доведення: .

3. Диференціал від невизначеного інтеграла дорівнює підінтегральному виразу: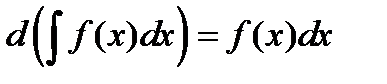

Доведення: .

4. Сталий множник можна виносити за знак інтеграла: .

5. Невизначений інтеграл від алгебраїчної суми двох функцій дорівнює алгебраїчній сумі цих інтегралів від цих функцій: .

Властивості № 4 і 5 перевіряються диференціюванням на основі властивості № 1. Властивість № 5 справедлива для довільного, скінченного числа доданків.

1. Якщо і- довільна функція, що має неперервну похідну, то .

Доведення: Внаслідок інваріантності форми першого диференціала і властивості 2 маємо:

Основні методи інтегрування.

1. Метод безпосереднього інтегрування.

Означення: Обчислення інтегралів за допомогою основних властивостей невизначеного інтеграла, таблиці інтегралів, називається безпосереднім інтегруванням.

Приклад: .

2. Метод підстановки (заміна змінної).

Теорема. Якщо - перервна функція на проміжку , тобто , , і нехай функція визначена і диференційована на проміжку , причому множина значень цієї функції є проміжок . Тоді справедлива формула: (1)