Определение. Бинарное отношение R, определенное на множестве А, называется отношением эквивалентности или просто эквивалентностью на множестве А, если R рефлексивно, симметрично и транзитивно.
Примеры отношений эквивалентности:
1) отношение равенства в произвольной системе множеств;
2) отношение равночисленности, то есть иметь одинаковое число элементов, в системе конечных множеств;
3) отношение «учиться в одной группе» в множестве студентов энергетического факультета;
4) пусть F: A → B – отображение. Отношение σ, определяемое следующим образом: 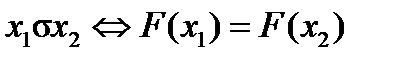 , является отношением эквивалентности на А. Оно называется ядерной эквивалентностью отображения F.
, является отношением эквивалентности на А. Оно называется ядерной эквивалентностью отображения F.
ПРИМЕР. Рассмотрим на множестве дробей Х= 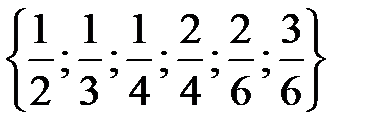 отношение равенства. Это отношение:
отношение равенства. Это отношение:
- рефлексивно, так как всякая дробь равна сама себе;
- симметрично, так как из того, что дробь 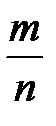 равна дроби
равна дроби 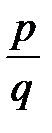 , следует, что дробь
, следует, что дробь 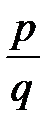 равна дроби
равна дроби 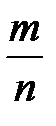 ;
;
- транзитивно, так как дробь 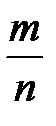 равна дроби
равна дроби 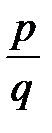 , и дробь
, и дробь 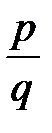 равна дроби
равна дроби 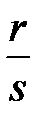 , следует, что дробь
, следует, что дробь 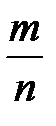 равна дроби
равна дроби 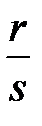 ;
;
Про отношение равенства дробей говорят, что оно является отношением эквивалентности.
Пусть σ – отношение эквивалентности на множестве А, и пусть 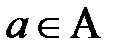 .
.
Определение. Множество всех таких элементов 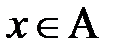 , что х σ а истинно, называют смежным классом множества А по эквивалентности σ, или классом эквивалентности, и обозначают [ а ] σ.
, что х σ а истинно, называют смежным классом множества А по эквивалентности σ, или классом эквивалентности, и обозначают [ а ] σ.
Теорема 3.3. Свойство I: 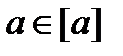 . Свойство II: если a σ b, то [ а ] = [ b ].
. Свойство II: если a σ b, то [ а ] = [ b ].
Лемма. Любые два смежных класса множества А по эквивалентности σ либо не пересекаются, либо совпадают.
Из леммы вытекает, что различные смежные классы не имеют общих элементов.
Определение. Совокупность всех различных смежных классов множества А по эквивалентности σ называется фактор-множеством множества А по эквивалентности σ и обозначается А /σ.
Определение. Каноническим отображением множества А на фактор-множестве А /σ по эквивалентности σ называется отображение, которое каждому элементу 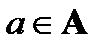 ставит в соответствие содержащий его смежный класс [ a ]σ.
ставит в соответствие содержащий его смежный класс [ a ]σ.
Очевидно, это каноническое отображение сюръективно.
Отношения эквивалентности произвольного множества тесно связаны с понятием разбиения этого множества.
ПРИМЕР. Рассмотрим отношение равенства дробей, заданное на множестве 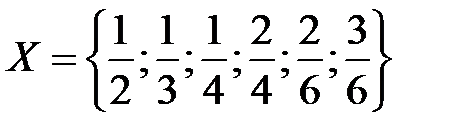
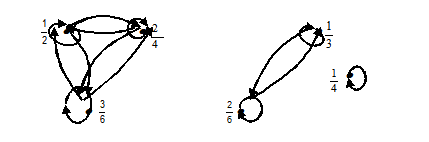
Рисунок 3.4 – Разбиение множества
Видим, что множество разбилось на три подмножества: 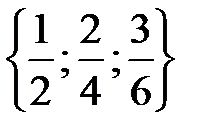 ,
, 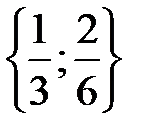 ,
, 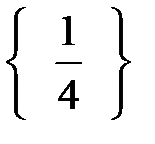 . Эти подмножества не пересекаются, а их объединение совпадает с множеством Х, т.е. имеет разбиение множества Х на классы. Так, мы установили, что отношению равенства на множестве дробей
. Эти подмножества не пересекаются, а их объединение совпадает с множеством Х, т.е. имеет разбиение множества Х на классы. Так, мы установили, что отношению равенства на множестве дробей 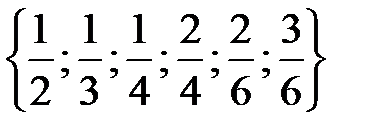 соответствует разбиению этого множества на классы эквивалентности, каждый из которых состоит из равных между собой дробей.
соответствует разбиению этого множества на классы эквивалентности, каждый из которых состоит из равных между собой дробей.
Определение. Разбиением (или расслоением) множества А называется система S непустых подмножеств множества А таких, что каждый элемент из А принадлежит одному и только одному подмножеству из системы S.
Подмножества из S называются смежными классами (или слоями) разбиения S.
Рассмотрим связи между отношениями эквивалентности некоторого множества и его разбиениями.
Теорема 3.4. Если σ – отношение эквивалентности на множестве А, то совокупность всех различных смежных классов множества А по эквивалентности σ является разбиением множества А.
Теорема 3.5. Пусть S – разбиение множества А, а σ — бинарное отношение на множестве А такое, что, по определению, х σ у (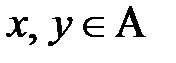 ) истинно тогда и только тогда, когда в S есть подмножество М, для которого
) истинно тогда и только тогда, когда в S есть подмножество М, для которого 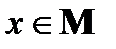 ,
, 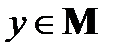 . Тогда σ – отношение эквивалентности на множестве А. Эта эквивалентность σ называется эквивалентностью, отвечающей разбиению S.
. Тогда σ – отношение эквивалентности на множестве А. Эта эквивалентность σ называется эквивалентностью, отвечающей разбиению S.
Теорема 3.6. Для любого множества А существует взаимно однозначное соответствие между множеством разбиений множества А и множеством отношений эквивалентности на А.
Определение. Отношение ρ на множестве А называется отношением порядка, если оно одновременно обладает свойствами антисимметричности и транзитивности.
Примеры отношений порядка:
- отношение «меньше» на множестве натуральных чисел;
- отношение «короче» на множестве отрезков.
Определение. Бинарное отношение ρ, определенное на множестве А, называется частичным порядком, или отношением частичного порядка, если оно удовлетворяет следующим условиям:
1) х ρ х для любого 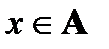 (рефлексивность);
(рефлексивность);
2) из х ρ у и y ρ z следует x ρ z для любых 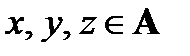 (транзитивность);
(транзитивность);
3) из х ρ у и у ρ х следует х=у для любых 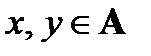 (антисимметричность).
(антисимметричность).
Определение. Множество А, на котором задан какой-нибудь частичный порядок, называется частично упорядоченным.
Примерами отношения частичного порядка являются: отношение 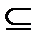 включения на множестве подмножеств некоторого множества; отношение ≤ на множестве действительных чисел; отношение «х делит у» на множестве натуральных чисел.
включения на множестве подмножеств некоторого множества; отношение ≤ на множестве действительных чисел; отношение «х делит у» на множестве натуральных чисел.
Частичный порядок на множестве А будем обозначать символом ≤, и если a ≤ b для некоторых элементов 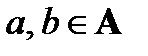 , то будем говорить, что а меньше или равно b, а также, что а содержится в b или равно b. Если a ≤ b и а ≠ b, то будем писать а < b и говорить, что а строго меньше b или а строго содержится в b.
, то будем говорить, что а меньше или равно b, а также, что а содержится в b или равно b. Если a ≤ b и а ≠ b, то будем писать а < b и говорить, что а строго меньше b или а строго содержится в b.
Определение. Элементы а, b множества А называются сравнимыми относительно частичного порядка ≤ на этом множестве, если a ≤ b или b ≤ a.
Определение. Пусть А – частично упорядоченное множество с частичным порядком ≤. Элемент 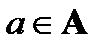 называется наибольшим элементом, если х ≤ а для любого
называется наибольшим элементом, если х ≤ а для любого 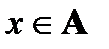 . Элемент
. Элемент 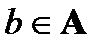 называется наименьшим элементом, если b ≤ х для любого
называется наименьшим элементом, если b ≤ х для любого 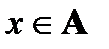 .
.
Частично упорядоченное множество может обладать или не обладать наименьшим или наибольшим элементом. Однако если частично упорядоченное множество обладает наибольшим (наименьшим) элементом, то он единственный.
Определение. Максимальным элементом частично упорядоченного множества А называется такой элемент 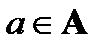 , что каждый элемент х из А либо не сравним с а, либо х ≤ а, т.е., другими словами, если А не содержит элементов, строго больших а.
, что каждый элемент х из А либо не сравним с а, либо х ≤ а, т.е., другими словами, если А не содержит элементов, строго больших а.
Определение. Минимальным элементом частично упорядоченного множества А называется такой элемент 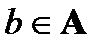 , что каждый элемент x из А либо не сравним с b, либо b ≤ х, т.е. если А не содержит элементов, строго меньших b.
, что каждый элемент x из А либо не сравним с b, либо b ≤ х, т.е. если А не содержит элементов, строго меньших b.
В отличие от наибольшего (наименьшего) элемента частично упорядоченное множество может содержать несколько максимальных (минимальных) элементов.
Лемма. Всякий наибольший элемент частично упорядоченного множества является максимальным, а всякий наименьший – минимальным.
Определение. Пусть а, b – элементы частично упорядоченного множества А. Элемент а называется непосредственно меньшим (непосредственно предшествующим) для элемента b, а b – непосредственно большим (непосредственно следующим) за а, если a < b и не существует элемента 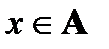 , который удовлетворял бы отношению a < х < b.
, который удовлетворял бы отношению a < х < b.
Определение. Частичный порядок на множестве А называется линейным порядком, если любые два элемента из А сравнимы относительно ≤.
Определение. Множество А, на котором задан какой-либо линейный порядок, называется линейно упорядоченным множеством, или цепью.
Примером линейно упорядоченного множества может служить множество всех действительных чисел с обычным отношением ≤.
Отметим, что в случае линейно упорядоченного множества его максимальный (минимальный) элемент является также наибольшим (наименьшим).
Теорема 3.7. Следующие свойства частично упорядоченного множества А равносильны:
1) (условие минимальности). Всякое непустое подмножество множества А является частично упорядоченным множеством, содержащим минимальные элементы;
2) (условие индуктивности). Если все минимальные элементы множества А обладают некоторым свойством Р и из того, что все элементы х из А, удовлетворяющие условию х < а, обладают свойством Р, вытекает, что элемент а также обладает свойством Р, то свойством Р обладают все элементы
Определение. Линейно упорядоченное множество, удовлетворяющее условию минимальности (а, следовательно, и остальным условиям теоремы), называется вполне упорядоченным множеством.
Определение. Элемент а вполне упорядоченного множества А, не имеющий непосредственно предшествующего, называется предельным.
Не следует думать, что все отношения делятся на отношения эквивалентности и отношения порядка. Существует огромное количество отношений, не являющихся ни отношениями эквивалентности, ни отношениями порядка.
 2020-04-12
2020-04-12 348
348







