Существуют отношения, которые свойством рефлексивности не обладают

Примеры отношений, которые свойством рефлексивности не обладают:

- отношение перпендикулярности на множестве отрезков (нет ни одного отрезка, о котором можно сказать, что он перпендикулярен самому себе);

- отношение «длиннее» для отрезков.

Определение. Отношение R на множестве А называется антирефлексивным, если о каждом элементе множества А можно сказать, что он не находится в отношении R с самим собой, то есть для любого 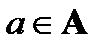 не выполняется aRa.

Определение. Отношение R на множестве A называется симметричным, если выполняется условие: из того, что элемент a находится в отношении R с элементом b, следует, что и элемент b находится в отношении R с элементом a, то есть для любых 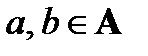  из аRb следует bRa.

Замечание. Граф симметричного отношения обладает особенностью: вместе с каждой стрелкой, идущей от a к b, граф содержит и стрелку, идущую от b к a. Справедливо и обратное утверждение. Граф, содержащий вместе с каждой стрелкой, идущей от a к b, и стрелку, идущую от b к a, является графом симметричного отношения.  

Примеры симметричных отношений:

- отношение параллельности на множестве прямых (если прямая х параллельна прямой у, то прямая у параллельна прямой х);

- отношение подобия треугольников (если треугольник F подобен треугольнику Р, то треугольник Р подобен треугольнику F).

- отношение перпендикулярности на множестве отрезков (если один отрезок перпендикулярен другому отрезку, то этот «другой» перпендикулярен первому);

- отношение «длиннее» для отрезков (если один отрезок равен другому отрезку, то этот «другой» равен первому).

ПРИМЕР. Рассмотрим отношение «длиннее» на множестве отрезков, которое свойством симметричности не обладает. Действительно, если отрезок х длиннее отрезка у, то отрезок у не может быть длиннее отрезка х. Про отношения «длиннее» говорят, что оно обладает свойством антисимметричности или просто антисимметрично.

Определение. Отношение R на множестве A называется антисимметричным, если для различных элементов a и b из множества A выполнено условие: если аRb и bRa влекут a = b.

Замечание. Граф антисимметричного отношения обладает особенностью: если вершины графа соединены стрелкой, то эта стрелка только одна. Справедливо и обратное утверждение: граф, вершины которого соединены только одной стрелкой, есть граф антисимметричного отношения.

Примеры антисимметричных отношений:

- отношение «длиннее» на множестве отрезков;

- отношение «больше» для чисел (если х больше у, то у не может быть больше х);

- отношение «больше на 2» для чисел (если х больше у на 2, то у не может быть больше на 2 числа х).

ПРИМЕР. Рассмотрим отношение «быть сестрой» на множестве детей одной семьи, которое не обладает ни свойством симметричности, ни свойством антисимметричности. Пусть в семье трое детей: Катя, Маша, и Толя. Тогда граф отношения» быть сестрой» будет таким:

                                 К ·                    · М

 

                                                     ·

                                                       Т

Рисунок 3.3 – Граф отношения «Быть сестрой»

 

Он показывает, что данное отношение не обладает ни свойством симметричности, ни свойством антисимметричности.

Определение. Отношение R на множестве A называется транзитивным, если выполняется условие: из того, что элемент a находится в отношении R с элементом b, а элемент b находится в отношении R с элементом c, то следует, что и элемент a находится в отношении R с элементом c, то есть для любых  из a R b и b R с следует а R с.

Замечание. Граф транзитивного отношения с каждой парой стрелок, идущих от a к b и b к c, содержит стрелку, идущую от a к c. Справедливо и обратное утверждение.

ПРИМЕР. Отношение ≤ на множестве R действительных чисел, а также отношение включения подмножеств некоторого множества являются рефлексивными и транзитивными, но не являются симметричными. Отношение < на множестве действительных чисел транзитивно, но не рефлексивно, не симметрично. Отношение «х является матерью у» не рефлексивно, не симметрично, не транзитивно.

Рассмотрим теперь свойства бинарных отношений на языке матриц.

Пусть R – бинарное отношение на множестве 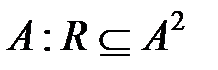. Отношение R:

· рефлексивно, если на главной диагонали матрицы отношения расположены только единицы;

· симметрично, если матрица симметрична относительно главной диагонали;

· антисимметрично, если в матрице все элементы вне главной диагонали являются нулевыми;

· транзитивно, если выполнено соотношение .

ПРИМЕР. Проверим, какими свойствами обладает отношение 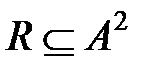, А ={1,2,3}, заданное графом отношения.

Составим матрицу отношения R:

Так как в матрице  на главной диагонали имеются нулевые элементы, отношение R не рефлексивно.

Несимметричность матрицы 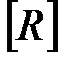 означает, что отношение R не симметрично.

Для проверки антисимметричности вычислим матрицу .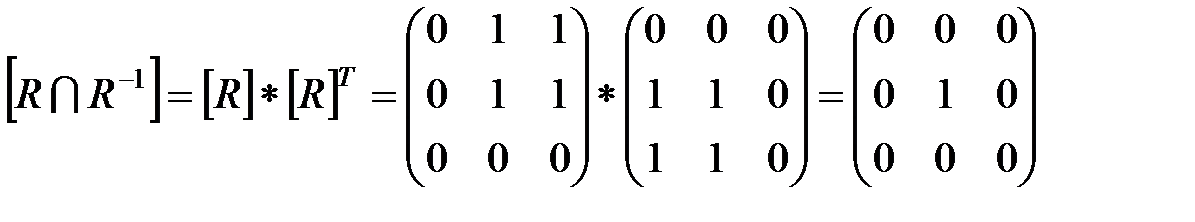

Поскольку в полученной матрице все элементы, стоящие вне главной диагонали, нулевые, отношение R антисимметрично.

Так как  (проверьте!), то , то есть R является транзитивным отношением.