Так как бинарные отношения, определенные на фиксированной паре множеств А, В, являются подмножествами декартового произведения А × В, то над ними можно производить операции объединения, пересечения и дополнения (в множестве А × В). Так, если R, S – два бинарных отношения, определенных па паре множеств А, В, то для любых 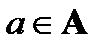 ,
, 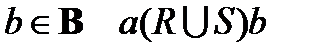 тогда и только тогда, когда aRb или aSb;
тогда и только тогда, когда aRb или aSb; 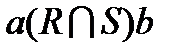 тогда и только тогда, когда aRb и aSb;
тогда и только тогда, когда aRb и aSb; 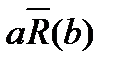 тогда и только тогда, когда не aRb.
тогда и только тогда, когда не aRb.
Помимо теоретико-множественных операций над отношениями важное значение имеют еще две операции над ними: обращение и умножение отношений.
Определение. Пусть 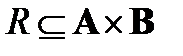 – бинарное отношение, определенное на паре множеств А, В. Отношением, обратным к бинарному отношению R, называется отношение, определенное на паре множеств В и А и состоящее из всех тех и только тех пар (b, а), для которых
– бинарное отношение, определенное на паре множеств А, В. Отношением, обратным к бинарному отношению R, называется отношение, определенное на паре множеств В и А и состоящее из всех тех и только тех пар (b, а), для которых 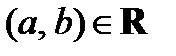 (
(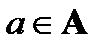 ,
, 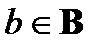 ).
).
Бинарное отношение, обратное к отношению R, обозначается R –1. Таким образом, 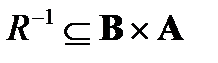 . Можно сказать, что (R -1)-1= R.
. Можно сказать, что (R -1)-1= R.
ПРИМЕР. Если R – бинарное отношение «х является родителем у», то R –1 – отношение «х является ребенком (сыном или дочерью) у».
Определение. Пусть 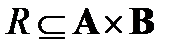 – бинарное отношение, определенное на паре множеств А, В, а
– бинарное отношение, определенное на паре множеств А, В, а 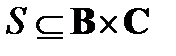 – бинарное отношение, определенное на паре множеств В, С. Произведением отношений R и S называется бинарное отношение, определенное на паре множеств А и С и состоящее из всех тех и только тех пар (а, с) (
– бинарное отношение, определенное на паре множеств В, С. Произведением отношений R и S называется бинарное отношение, определенное на паре множеств А и С и состоящее из всех тех и только тех пар (а, с) (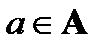 ,
, 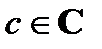 ), для которых существует элемент х из В такой, что aRx и xSc.
), для которых существует элемент х из В такой, что aRx и xSc.
Произведение бинарных отношений 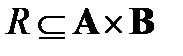 и
и 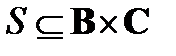 обозначим через RS. Таким образом,
обозначим через RS. Таким образом, 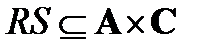 и a (RS) c тогда и только тогда, когда существует элемент
и a (RS) c тогда и только тогда, когда существует элемент 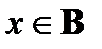 такой, что aRx и xSc.
такой, что aRx и xSc.
Кроме того, отношения могут задать новое отношение, называемое ком позицией.
R 1° R 2= R ={(a, b, c)|(a, b)Î R 1 и с Î А и a R 1 b R 2 c }. Последовательная композиция отношения с самим собой называется степенью отношенияR ° R ° R °…° R = R n.
Имеем: R 0= I; R 1= R; R ° R = R 2;…… R ° Rn -1= Rn.
Утверждение. Если некоторая пара (a, b) принадлежит какой-либо степени отношения R на множестве А мощности n, то эта пара принадлежит и степени R не выше n- 1. R Í A 2& | A |= n Þ (" a, b Î A) ($ k | aRkb Þ k < n).
Определение. Композиция отношения с обратным называется ядром отношения и обозначается как ker R=R° R-1. Ядро отношения само является отношением на А.
Теорема 3.1. Пусть 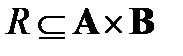 ,
, 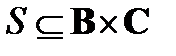 ,
, 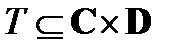 – бинарные отношения. Тогда произведения (RS) T и R (ST)определены и (RS) T = R (ST). То есть умножение бинарных отношений ассоциативно.
– бинарные отношения. Тогда произведения (RS) T и R (ST)определены и (RS) T = R (ST). То есть умножение бинарных отношений ассоциативно.
Теорема 3.2. Пусть 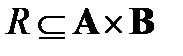 ,
, 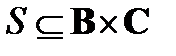 – бинарные отношения. Тогда выражения (RS)–1 и S –1 R –1 определены и имеет место равенство (RS)–1 = S –1 R –1.
– бинарные отношения. Тогда выражения (RS)–1 и S –1 R –1 определены и имеет место равенство (RS)–1 = S –1 R –1.
Рассмотрим операции бинарных отношений на языке матриц бинарного отношения.
1. Если 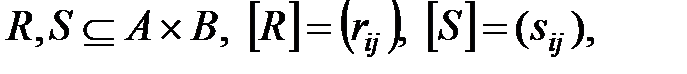 то
то 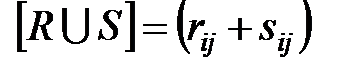 и
и 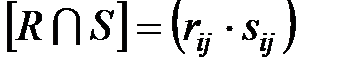 , где сложение осуществляется по правилам 0+0=0, 1+1=0+1=1+0=1, а умножение – обычным способом. Итак,
, где сложение осуществляется по правилам 0+0=0, 1+1=0+1=1+0=1, а умножение – обычным способом. Итак, 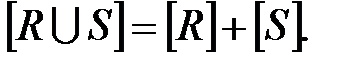
2. Матрица 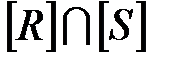 получается перемножением соответствующих элементов из
получается перемножением соответствующих элементов из 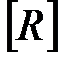 и
и 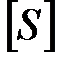 :
: 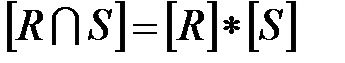 .
.
3. Если 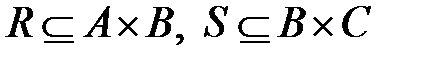 , то
, то 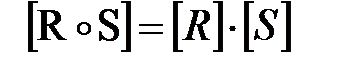 , где умножение матриц производится по обычному правилу умножения матриц, но произведение и сумма элементов – по определённым в свойстве 1 правилам.
, где умножение матриц производится по обычному правилу умножения матриц, но произведение и сумма элементов – по определённым в свойстве 1 правилам.
4. Матрица обратного отношения R-1 равна транспонированной матрице отношения R: 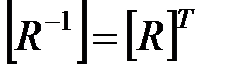 .
.
5. Если 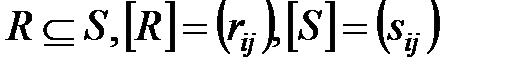 , то
, то 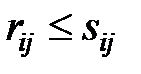 .
.
6. Матрица тождественного отношения I A единична:
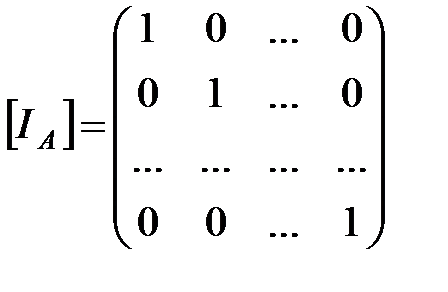
ПРИМЕР. Пусть 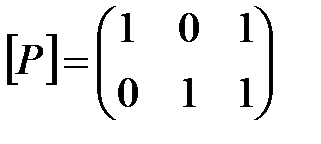
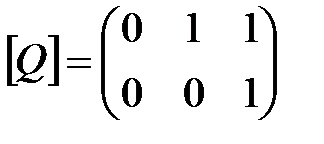 – матрицы отношений P и Q.
– матрицы отношений P и Q.
Тогда 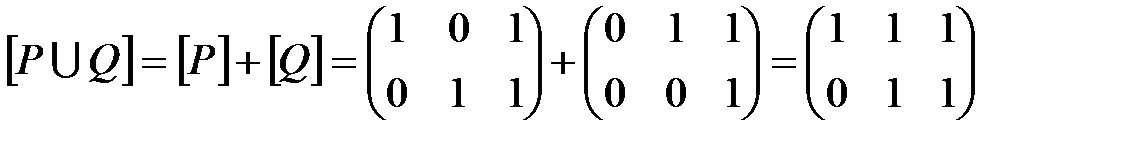
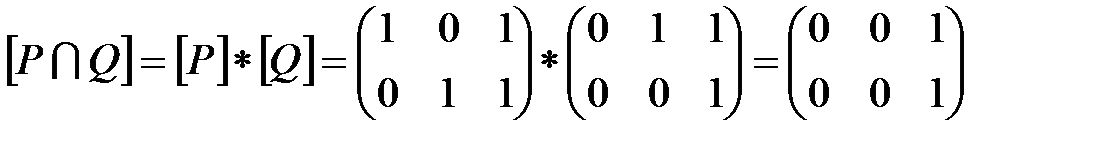
ПРИМЕР. Если 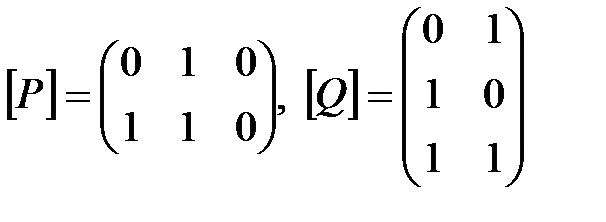 , то
, то 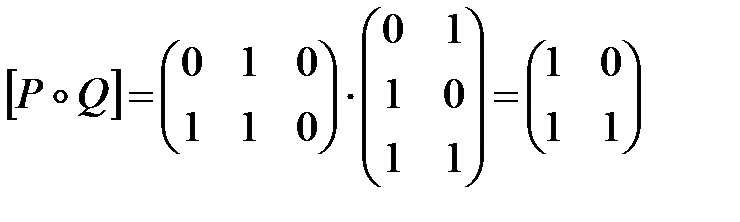
 2020-04-12
2020-04-12 1116
1116








