Тема 3. Машины для перемешивания жидких продуктов

В самых различных отраслях пищевой промышленности возникает необходимость в перемешивании жидких продуктов. Это бывает необходимо делать в случаях смешивания двух или нескольких жидкостей, для растворения или равномерного распределения твердых продуктов в жидкости, для интенсификации тепловых процессов и химических реакций, для получения или поддержания определенной температуры или консистенции жидкостей, для сохранения определенного технологического состояния эмульсий и суспензий и т.д. Для этих целей в промышленности применяются различные типы перемешивающих машин или, как их часто называют, мешалок.

 

Классификация мешалок

В связи с применением большого числа различных топов мешалок целесообразно их классифицировать по ряду существенных признаков, характеризующих как сам процесс идущий в этих машинах, так и их конструктивные особенности. Они разделяются:

По назначению: применение в аппаратах для смешивания, растворения, интенсификации технологических процессов и темперирования.

По ритму работы: на машины периодического и непрерывного действия.

По характеру движения жидкости в сосуде: радиальное, осевое, тангенциальное и смешанное.

По отношению к тепловым процессам в аппаратах со стеночной поверхностью теплообмена, с погружной поверхностью теплообмена и без использования тепловых процессов.

По характеру обработки жидкости: смешивание одновременно во всем объеме жидкости, смешивание в части объема и пленочное смешивание.

По виду сосуда: вертикальные, горизонтальные, наклонные, специальные и без использования емкости.

По принципу работы: механические, пневматические, эжекторные, циркуляционные и специальные.

Из группы мешалок, объединенных последним признаком, следует особо выделить механические, как получившие наибольшее распространение в промышленности, которые, в свою очередь, по конструктивным признакам можно разделить: на лопастные, рамные, планетарные, пропеллерные, турбинные и тарельчатые.

В данном пособии рассмотрены расчеты некоторых параметров, только лопастных наиболее часто применяемых типов механических мешалок. В настоящее время уже созданы более рациональные конструкции механических мешалок. В будущем эти конструкции будут модернизированы, улучшаться их параметры, они станут более эффективными и экономичными. Однако, всегда при проектировании любой мешалки, механической или немеханической, неизбежно встанет вопрос о том, какую скорость необходимо сообщить жидкости, т.е. как определить предельную скорость рабочего органа.

 

Определение скорости вращения лопасти

Рассмотрим наиболее простой, но и более распространенный в промышленности тип механической мешалки – лопастной (см. рис. 3.1) и определим для нее предельную частоту вращения лопасти. Для этого вначале сделаем допущение, вполне приемлемое для инженерного расчета, что жидкость в емкости вращается с угловой скоростью, равной угловой скорости вращения лопасти, без скольжения.

Представим себе, что имеется цилиндрическая емкость с размерами: R – внутренним радиусом и Н – высотой емкости.

Емкость наполнена жидкостью, уровень которой в спокойной состоянии равен высоте h. В емкость опущена лопасть. При вращении лопасти жидкость также начинает вращаться и на ее поверхности образуется параболическая воронка: в центре жидкость опускается до высоты h _min, а по краям поднимается до высоты h _max.

 

             

Рис. 3.1. Схема к расчету скорости лопасти лопастной мешалки

Выделим на поверхности полученного таким образом параболоида частицу или элементарную площадку с координатами Х и У, причем ось Х направлена по дну емкости, а ось У – по оси емкости. Соответственно проекции этой площадки на координатные оси будут равны d _x и d _y. Проведем касательную к поверхности параболоида в этой точке, которая окажется наклонной к оси Х под углом a.

Таким образом, соотношение между проекциями этой площадки будет таково:

                                                                                           (3.1)

На эту элементарную площадку действуют следующие силы:

1) Сила тяжести G, направленная вертикально вниз и равная произведению массы m на ускорение свободно падающего тела g:

                                  G = m × g

2) Так как площадка вращается в горизонтальной плоскости с некоторой угловой скоростью w, то на нее действует центробежная сила инерции Р, направленная горизонтально от центра вращения и равная произведению массы m на центростремительное ускорение a _цс.

                           P = m × a_цс или P = m × w²x,

так как a_цс = w²x, где х – радиус вращения площадки.

3) Равнодействующая сила N, являющаяся суммарной силой от сложения силы тяжести G с силой инерции Р. Она направлена по нормали к параболоиду в месте расположения элементарной площадки, т.е. перпендикулярно проведенной ранее касательной. Это является свойством всех частиц жидкости, расположенных на поверхности параболоида, у которых равнодействующая от сил тяжести и инерции направлена по нормали к поверхности. Именно поэтому на поверхности вращающейся жидкости и образуется параболическая воронка.

Таким образом, из рассмотренного пучка сил и известного угла a можно записать следующее соотношение:

                                                                                          (3.2)

Рассматривая два полученных соотношения (3.1) и (3.2) видно, что оба они выражены относительно одной и той же величины - tg a.

Приравняв их можно записать:

                                                                                            (3.3)

 

Подставив в полученное уравнение значение сил Р и G, выразим его относительно величины d _y:

                      или                          (3.4)

Полученное дифференциальное уравнение проинтегрируем

                          или ,                    (3.5)

так как

                                .

Чтобы определить значение постоянной С, необходимо переменную Х приравнять к нулю, то есть подставить значение Х = 0 в уравнение (3.5). Тогда получим, что у = С, но при Х = 0 ордината у = h_min (см. рис. 3.1). Таким образом имеем, что постоянная интегрирования С выражает значение ординаты вершины параболоида h_min. Значит выражение (3.5) можно записать так:

                                                                               (3.6)

Пользуясь полученным уравнением (3.6), можно при необходимости точно построить параболический профиль воронки, зная величины h_min и w, задаваясь величиной Х и рассчитывая значения У.

При предельном значении Х = R, очевидно, ордината у = h_max (см. рис. 3.1). Подставив эти значения в уравнение (3.6) получим:

                                                                          (3.7)

Полученное уравнение (3.7) имеет две неизвестные величины h _min и w Поэтому его нельзя использовать для нахождения предельной скорости вращения жидкости (лопасти) и необходимо найти другое уравнение, содержащее эти величины.

Для этого определим объем жидкости в емкости V. Он очевидно, равен:

                                     ,

где h – уровень жидкости в спокойном состоянии.

Но при вращении жидкости ее объем V не изменяется, однако определить его можно как разность двух объемов: объема цилиндра V _ц с высотой h _max и объема параболоида V _п, то есть:

                     V = V_ц – V_п или pR²h = pR²h_max – V_п                    (3.8)

Чтобы определить объем параболоида, представим его на схеме (рис. 3.2), подобной рис. 3.1.

Рис. 3.2. Схема к расчету объема параболоида

Представим себе, что параболоид состоит из наложенных друг на друга соосных элементарных дисков, имеющих радиус Х и бесконечно малую высоту dy. Объем одного такого элементарного диска будет равен: dV = px2dy. Объем параболоида V п будет равен сумме объемов бесконечно большого числа элементарных дисков, составляющих этот параболоид в пределах изменения переменной У от h min до h max, или в пределах изменения переменной Х соответственно от 0 до R. То есть, имеем дифференциальное уравнение:

 

       , или                                        (3.9)

В этом уравнении две переменные величины Х и У, следовательно для его решения необходимо одну из переменных заменить другой. Для этого используем уравнение (3.4) дающее значение величины dy относительно Х. Одновременно изменим и пределы интегрирования: вместо пределов по У возьмем пределы по Х. Таким образом, подставив уравнение (3.4) в уравнение (3.9) и изменив пределы интегрирования, получим:

                              ,

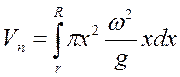или

                                                                             (3.10)

Используя применявшееся ранее для интегрирования уравнений (2.49) и (3.5) табличное значение интеграла , проинтегрируем уравнение (3.10) и получим

                            

Сделаем подстановку пределов интегрирования и получим:

                                                                                   (3.11)

Подставим полученное выражение (3.11) в уравнение (3.8):

                                                        (3.12)

Упростим это уравнение, сократив обе его части на величину pR² и выразив его относительно h _max, получим:

                                                                           (3.13)

Приравняв правые части уравнений (3.7) и (3.13) как выражающие одну и ту же величину – h _max и найденные независимым образом:

                                                        (3.14)

Легко заметить, что величина  является суммой двух одинаковых величин, т.е.  поэтому от левой и правой части уравнения (3.14) можно отнять одну и ту же величину, а именно . Тогда уравнение (3.14) примет вид:

             , или                    (3.15)

Сравнивая полученные в итоге два уравнения (3.13) и (3.15), легко заметить, что параболическая воронка на поверхности вращающейся жидкости характеризуется двумя параметрами – высотами h _min и h _max. Причем высота h _max равна уровню жидкости в спокойном состоянии, к которому прибавляется некоторая величина , а высота вершины воронки h _min равна тому же уровню h, от которого вычитается та же самая величина . Эта величина зависит как от радиуса емкости, так и в большей степени от скорости вращения жидкости.

Теперь можно определить предельную частоту вращения лопасти мешалки, но для этого необходимо задаться конкретными условиями:

1) Условие невыплескивания жидкости из емкости.

Для этого, очевидно, необходимо, чтобы высота параболической воронки h _max была бы меньше высоты емкости Н. То есть это условие можно записать так (см. рис. 3.1)

                                         h_max < Н.

Подставив в это условие значение h _max из уравнения (3.13) получим:

                                                                                   (3.16)

Решив это неравенство относительно w, определим предельную угловую скорость лопасти w _нв, (с^-1), которую она может иметь для того, чтобы жидкость в емкости размерами R и Н (м), налитая до уровня h (м), не выплескивалась через край емкости:

                                                                            (3.17)

2) Условие необнажения лопасти мешалки.

Это условие также имеет практический смысл. Требуется обеспечить такую скорость, чтобы верхний край лопасти не оказался выше уровня воронки, то есть, чтобы нижний уровень воронки в центре был бы выше плоскости верхнего края лопасти – h ₁ (см. рис. 3.1)

                                   

Для этого условия приемлемо уравнение (3.15):

                                                                                  (3.18)

Решив это неравенство, определим также предельную угловую скорость лопасти w _нл (с^-1), которую она может иметь для того, чтобы ее верхний край не оказался выше уровню перемешиваемой жидкости

                                                                            (3.19)

3) Условие необнажения дна емкости.

В случае применения специальных типов мешалок, особенно если процесс перемешивания связан с нагреванием жидкости в этой же емкости, может быть поставлено и такое условие.

Для этого случая, очевидно, будет справедливо следующее неравенство h _min > 0 (см. рис. 3.1).

Значит, в данном случае также можно воспользоваться уравнением (3.15) и составить такое неравенство:

                                                                                   (3.20)

Решив его относительно угловой скорости, определим предельную угловую скорость лопасти w ₀ (с^-1) для этого случая:

                                                                                     (3.21)

Таким образом, полученные уравнения (3.13) и (3.15) и (3.21) позволяют определить любую предельную угловую скорость лопасти (а значит и ее частоту вращения, так как 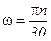 (с^-1) и задаваясь определенным условием, которое необходимо выполнить для того, чтобы процесс перемешивания жидкости в мешалке определенной конструкции протекал нормально.

Полученные соотношения позволяют также решать целый круг задач, связанных с определением одних параметром при известных других. Так, например, если задана скорость вращения лопасти, то по ним можно вести расчет размеров емкости или уровня жидкости, расположения лопастей и т.д.