1. Диференціювання функцій від однієї змінної.
2. Дослідження функцій за допомогою похідних.
3. Економічний сенс похідної.
5.1. Диференціювання функцій від однієї змінної
Означення. Нехай y = f (x) ‑ деяка функція; x ‑ деяка точка з області визначення y = f (x). Похідною функції y = f (x) у точці x називається границя відношення приросту функції до приросту аргументу, якщо приріст аргументу довільним чином прямує до нуля:
 (5.1)
(5.1)
Використовують також позначення
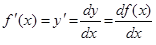 .
.
Наведемо таблицю похідних від елементарних функцій:
C ¢=0;
x ¢ =1;
(x n)¢ = nx n-1 , у тому числі 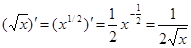 ;
;
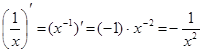 ;
;
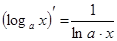 , у тому числі
, у тому числі 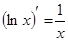 ;
;
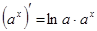 , у тому числі
, у тому числі 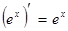 ;
;
(sin x)¢ = cos x; (cos x)¢ = - sin x;
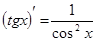 ;
; 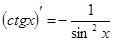 ;
;
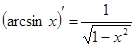 ;
; 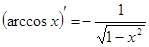 ;
;
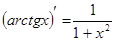 ;
; 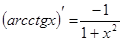 ;
;
Є такі правила обчислення похідних:
(u + v)¢ = u ¢ + v ¢ ‑ похідна від суми;
(uv)¢ = u ¢ v + uv ¢ ‑ похідна від добутку;
 ‑ похідна від частки;
‑ похідна від частки;
[ f (g (x))]¢ = f ¢(g (x))× g ¢(x) похідна від складної функції.
Приклади. Обчислити похідну від функції y = f (x) (продиференціювати функцію y = f (x)):
1) f (x) = 3 x 2 + e x;
f ¢(x) = 3×2 x + e x;
2) f (x) = 3 e -2x + 4lg x;
f ¢(x) = 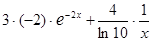 ;
;
3) f (x) = 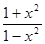 ;
;
f ¢(x) = 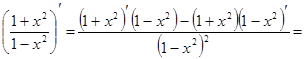
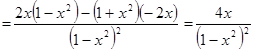 ;
;
4) f (x) =  ;
;
f ¢(x) =  ;
;
5) f (x) = sin2 x = (sin x)2;
f ¢(x) = (2sin x)×(sin x)¢ =2sin x ×cos x =sin2 x;
6) f (x) = sin x 2 = sin (x 2);
f ¢(x) = (cos(x 2))×(x 2)¢ = 2 x cos x 2;
7)  ;
;
f ¢(x)= (1/4)(1-sin3 x)-3/4×(-cos3 x)×3.
Приклад. Обчислити другу похідну від функції y (x) = x 3 + sin x:
y ¢¢(x) = (y ¢(x))¢ = (x 3+sin x) ¢¢ =
= (3 x 2+cos x) ¢ =6 x – sin x.
Нагадаємо також, що функція y = f (x) називається диференційовною в точці x0, якщо в цій точці існує похідна y ¢= f ¢(x).
Функція, диференційовна в деякій точці (на деякому відрізку) є неперервною в цій точці (на цьому відрізку).
5.2. Дослідження функцій за допомогою похідних
Означення. Функція y = f (x) має мінімум (максимум) у точці x 0, якщо існує такий окіл точки x0, що для всіх точок x ¹ x 0 цього околу виконується нерівність f (x 0)< f (x) (f (x 0)< f (x)).

 y
y

 x 0 x
x 0 x
Рис. 5.1.
Функція, показана на рис. 5.1, має два мінімуми та три максимуми. Нагадаємо, що поняття мінімуму та максимуму об’єднані в термін “екстремум”.
Теорема (необхідна умова існування екстремуму). Якщо диференційовна функція f (x) в точці x 0 має екстремум, то в цій точці похідна f ¢(x 0) =0.
Теорема. Якщо на деякому відрізку [ a; b ] похідна f ¢(x) від деякої функції є додатною (від’ємною), то на цьому відрізку функція f (x) зростає (спадає)
Теорема (перша достатня умова існування екстремуму). Якщо похідна f ¢(x) від деякої диференційоної функції f (x) в точці x = x 0 дорівнює нулю і при x < x 0 похідна f ¢(x)>0, а при x > x 0 похідна f ¢(x)<0, то точка x 0 є точкою максимуму. Якщо ж похідна f ¢(x) в деякому околі точки x 0 змінює знак з від’ємного на додатний, то точка x 0 є точкою мінімуму.
Теорема (друга достатня умова існування екстремуму). Якщо в точці x 0 диференційовної функції y = f (x) перша похідна f ¢(x)=0, а друга f ¢¢(x)<0, то в цій точці є максимум (мінімум, якщо f ¢¢(x)>0).
Поняття мінімуму та максимуму не треба плутати з поняттями найбільшого та найменшого значень функції на деякому інтервалі.
Зазначимо, що умова f ¢(x)=0 не є достатньою для існування екстремуму функції y = f (x).
Нехай y = f(x) ‑ деяка функція та (x 0; y 0) ‑ точка з області визначення цієї функції. Проведемо через точку (x 0; y 0) дотичну до кривої (рис. 5.2).



 y y = f (x)
y y = f (x)

 D y
D y

 d y
d y
 d x =D x
d x =D x
 a
a
 x 0 x
x 0 x
Рис. 5.2.
Рівняння цієї дотичної – це пряма
y = f (x 0) + f ¢(x 0)(x - x 0) (5.2)
Величина f ¢(x 0) = k = tga є нахилом кривої y = f (x) в точці x 0.
Означення. Диференціалом від функції y = f (x) називається вираз dy = f ¢(x) dx, де dx = D x ‑ приріст аргументу (рис. 5.2).
Приклад. Нехай y = ln(x 2+1).
Тоді 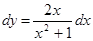 .
.
Приклад. Знайти екстремуми та інтервали зростання і спадання функції y = x 3 – 6 x 2 +9 x.
Знаходимо похідну y ¢ =3 x 2 – 12 x +9.
Розв’язуємо рівняння 3 x 2 – 12 x +9=0, звідки x 1=1; x 2=3.
Досліджуємо знаки першої похідної
| Інтервал | (-∞; 1) | 1 | (1; 3) | 3 | (3; +∞) |
| Знак f ¢(x) | + | 0 | - | 0 | + |
| Поведінка y = f (x) | Зростає | Максимум | Спадає | Мінімум | Зростає |
Точки x 1=1 та x 2=3 можна також дослідити згідно з другою достатньою умовою екстремуму:
y ²(x) = 6 x – 12;
y ²(1) = - 6 < 0, отже, в точці x =1 функція y = x 3 – 6 x 2 +9 x досягає максимуму;
y ²(3) = 6 > 0, отже, в точці x =3 ця функція має мінімум.
Означення. Функція f (x) називається випуклою (випуклою вверх) на відрізку [ a; b ], якщо на цьому інтервалі її графік розташований нижче від її дотичної (рис. 5.3,а). Функція f(x) називається увігнутою (випуклою вниз), якщо на [ a; b ] цей графік розташований нижче від дотичної (рис. 5.3,б).
 |  |
 y y
y y
 | |||
 | |||

 a b a b
a b a b
а x б x
Рис. 5.3.
Теорема (достатня умова випуклості). Якщо у всіх точках інтервалу [ a; b ] друга похідна f ²(x) двічі диференційовної функції y = f (x) є додатною f ²(x)>0, то функція y = f (x) є увігнутою на [ a; b ]. Якщо f ²(x)<0, то функція y = f (x) випукла на інтервалі [ a; b ].
Означення. Точка x 0, у якій функція y = f (x) змінює увігнутість на опуклість (або навпаки), називається точкою перегину функції y = f (x) (рис. 5.4).
Теорема (достатня ознака існування точки перегину). Якщо в точці x 0 існує перша похідна f ¢(x) і f ²(x)=0, причому друга похідна f ²(x) змінює знак, то точка x 0 є точкою перегину функції y = f (x) (рис. 5.4).

 y
y
 |  | ||||
 | |||||
 x 0 x
x 0 x
Рис. 5.4.
Приклад. Знайти інтервали випуклості та увігнутості функції y = x 3 ‑ 6 x 2 + 9 x.
Друга похідна y ²(x)=6 x -12 дорівнює нулю в точці x =2. Тому визначимо знаки цієї другої похідної на інтервалах (-∞;2) та (2;∞).
| Аргумент x | (-∞;2) | 2 | (2;∞). |
| Друга похідна y ²(x) | <0 | 0 | >0 |
| Функція y = f (x) | Випуклість | Перегин | Увігнутість |
Отже, функція y (x) є випуклою на інтервалі (-∞;2), у точці x =2 має перегин, а на інтервалі (2;∞) увігнута.
Приклад. Дослідити властивості логістичної кривої (рис. 4.12).
Логістичною функцією описують еволюцію продажу на ринку нового товару. Загальний вигляд логістичної функції (кривої) такий:  . Дослідимо конкретну логістичну функцію вигляду
. Дослідимо конкретну логістичну функцію вигляду 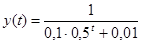 .
.
При t =0 маємо y(0)= 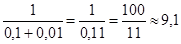 .
.
Знайдемо першу похідну від функції 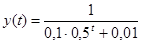 :
:
 . Оскільки для всіх t вираз 0,5t є завжди додатним, то перша похідна y ¢(x) ніколи не перетворюється в нуль, отже, логістична крива екстремумів не має.
. Оскільки для всіх t вираз 0,5t є завжди додатним, то перша похідна y ¢(x) ніколи не перетворюється в нуль, отже, логістична крива екстремумів не має.
Знайдемо другу похідну від y(t), тобто обчислимо
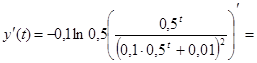
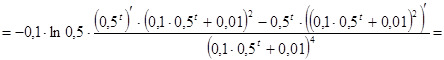

Розв’яжемо рівняння y ²(t) = 0 на інтервалі t >0, тобто рівняння
0,01-0,1×0,5t = 0,
звідки 0,5t = 0,1;
t lg0,5 = lg0,1;
t (-lg2) = -1;
t 0 = 1/lg2» 3,32.
Отже, при t 0=3,32 логістична крива має перегин. Значення y (t 0) в точці перегину 
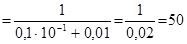 .
.
На інтервалі 0< t < t 0 логістична функція увігнута (кількість проданого товару залежно від часу зростає щораз швидше). Проте на нескінченному інтервалі t 0< t функція є випуклою (кількість проданого товару хоча й зростає, проте це зростання уповільнюється).
Приклад. Витрати на споживання деяких товарів (другої потреби) залежно від доходу описує функція Торнквіста  (a, b, c >0). Дослідимо цю функцію (рис. 4.13).
(a, b, c >0). Дослідимо цю функцію (рис. 4.13).
Похідна  завжди є додатнью на інтервалі z >0.
завжди є додатнью на інтервалі z >0.
Друга похідна 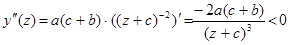 від’ємна.
від’ємна.
Отже, витрати на споживання y збільшуються зі зростанням доходу z, проте швидкість цього зростання зменшується (граничні витрати зменшуються).
Обчислимо також 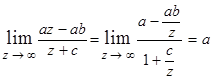 .
.
Отже, витрати на споживання цього товару не можуть перевищити a.
Приклад. На інтервалі (0,1; 0,5) залежність розміру надходжень до бюджету y від ставки оподаткування x описує крива (функція) Лаффера (рис. 5.5):
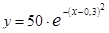 .
.
Дослідимо цю функцію, обчисливши першу та другу похідні:
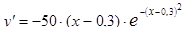 ;
;
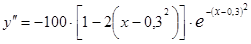 .
.
 y
y



 50
50
 0,3 x
0,3 x
Рис. 5.5.
Легко бачити, що при x =0,3 похідна y ¢(x)=0, причому друга похідна y ²(x)>0. Отже, ставка оподаткування x =0,3 = 30% в нашому прикладі дає найбільше надходження до бюджету.
Із рівняння y ²(x) = 0 знаходимо точки перегину кривої
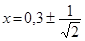 .
.
5.3. Економічний сенс похідної
Покажемо, як деякі економічні показники (граничне значення, темп приросту та еластичність) обчислюютьза допомогою похідної.
Означення (економічне). Граничним значенням My(x) показника y = y (x) називається приріст цього показника унаслідок додаткового збільшення аргументу x.
Нехай D x ‑ приріст цього аргументу, а D y ‑ приріст показника. Тоді  . Якщо y=y (x) є неперервною фукцією від x, то, перейшовши до границі, отримуємо
. Якщо y=y (x) є неперервною фукцією від x, то, перейшовши до границі, отримуємо 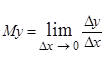 , тобто
, тобто
My (x) = y ¢(x). (5.3)
Приклад. Випуск продукції Q залежно від затрат x описує функція 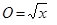 (рис. 5.6).
(рис. 5.6).
Тоді граничний продукт  .
.
Тепер 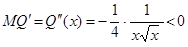 , отже зі збільшенням затрат граничний продукт зменшується.
, отже зі збільшенням затрат граничний продукт зменшується.

Q (випуск)





 dQ
dQ
 dx
dx

x (затрати)
Рис. 5.6.
Приклад. Корисність U від споживання деякого блага x задана функцією U=U (x)= ln(1+ x) (рис. 5.7). Тоді гранична корисність 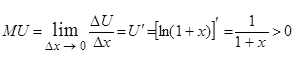 . Похідна M U¢= U ²(x)=
. Похідна M U¢= U ²(x)=  .
.
Зі зростанням кількості спожитих благ їхня гранична корисність зменшується.
 U (корисність)
U (корисність)



 dU
dU

 dx
dx

x (кількість благ)
Рис. 5.7.
Означення (економічне). Темпом приросту Ty (t) величини y = y (t) називається відносна зміна значення y за деякий проміжок часу.
Нехай час t змінився на проміжок D t.
Тоді 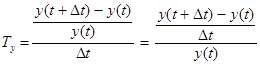 .
.
При D t ®0 маємо 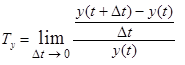 , тобто
, тобто 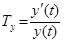 . (5.4)
. (5.4)
Приклад. Зміну кількості населення деякої країни описує функція P = 100000000 e 0,02 t . Тоді темп приросту цього населення
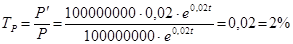
(протягом кожного наступного року кількість населення зростає на 2% по відношенню до попереднього).
Означення (економічне). Еластичністю Ey (x) показника y = y (x) за аргументом x називається відношення відносної зміни цього показника до відносної зміни аргументу.
Отже, 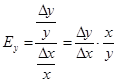 . Перейшовши до границі при D x ®0, отримуємо
. Перейшовши до границі при D x ®0, отримуємо
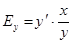 (5.5)
(5.5)
Приклад. Попит Q на деякий товар в залежності від його ціни p описує залежність 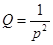 (рис. 5.8).
(рис. 5.8).
 p (ціна)
p (ціна)

 Крива попиту
Крива попиту

 D p
D p

 D Q
D Q
Q (величина попиту)
Рис. 5.8.
Визначимо еластичніть цього попиту. Згідно з отриманою формулою 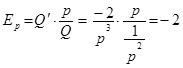 . Отже, зі збільшенням ціни на 1% попит на товар зменшиться на 2%. У разі зменшення ціни в 1,2 раза попит збільшиться в 2,4 раза.
. Отже, зі збільшенням ціни на 1% попит на товар зменшиться на 2%. У разі зменшення ціни в 1,2 раза попит збільшиться в 2,4 раза.
 2020-04-12
2020-04-12 83
83







