Тема 5: «Потери напора на трение»

1. Зависимость потерь напора от видов движения.

При движении жидкости величина потерь напора на трение может зависеть от следующих факторов:

1) Параметров трубопровода (диаметра d, длины l, средней высоты выступов шероховатости k на внутренних стенках трубы);

2) Свойств жидкости (плотности ρ, кинематической μ и динамической ν вязкости);

3) Средней скорости потока v.

Гидравлические сопротивления подразделяют на путевые h_l, проявляющиеся на всём протяжении потока, и местные h_м, проявляющиеся на коротких, ограниченных участках в определённом месте.

2. Ламинарный режим и его закономерности: распределение скоростей по живому сечению, потери напора. Формула Пуазёйля, Дарси-Вейсбаха.

Рассмотрим установившееся ламинарное движение жидкости в круглой трубе в условиях вполне сформировавшегося потока, т. е. полагая, что начальное сечение потока находится на расстояния от входа в трубу, достаточном для обеспечения устойчивого распределения скоростей в поперечном сечении. Найдём закон, по которому распределяются скорости по поперечному сечению трубы.

Как известно, ламинарное движение имеет слоистый характер и происходит без перемешивания частиц. Один слой движется по другому слою, причём между ними возникает сила трения, напряжение τ которой определяется законом вязкости Ньютона:

С другой стороны, для слоя жидкости на расстоянии y от стенки трубы касательное напряжение определяется формулой:

Следовательно:

Обозначив через а расстояние от оси трубы до рассматриваемого слоя жидкости (a=r-y), приведём уравнение к виду:

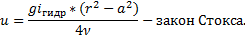
При ламинарном режиме движения жидкости в цилиндрической трубе круглого сечения распределение местных скоростей по радиусу имеет параболический характер. Максимальная скорость имеет место на оси трубы, т. е. при r=0:

Отношение скорости в рассматриваемой точке (местной скорости) к максимальной:

Это отношение зависит от положения рассматриваемой точки и не зависит от расхода, рода жидкости и материала стенок трубы. Расход жидкости в трубе можно найти путём суммирования элементарных расходов, проходящих через кольцевые площадки радиусом а и шириной da, т. е. из выражения

После подстановки вместо u его значения из уравнения Стокса получим:

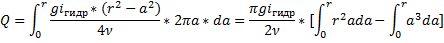
Средняя скорость потока:

Следовательно: .

Т. о., средняя скорость при ламинарном движении жидкости в трубе равна половине максимальной. Вычислим значение коэффициента Кориолиса; он имеет выражение:

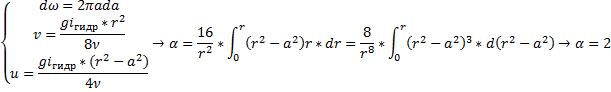
Т. о., кинетическая энергия ламинарного потока вдвое больше кинетической энергии, подсчитанной по средней скорости.

Формула Дарси-Вейсбаха: установлена экспериментально, характеризует величину потерь напора по длине.

λ=f(Re, Δ/d) – коэффициент гидравлического трения, или коэффициент Дарси.

Δ/d – относительная шероховатость.

Формула Пуазёйля: характеризует потери напора при ламинарном движении. Для жидкости в круглой трубе находим сначала выражение для гидравлического уклона в виде:

Или:

Заменяя абсолютную (динамическую) вязкость  через кинематическую ν, получаем формулу, называемую формулой Пуазёля-Гагена:

Потери напора на трение при ламинарном режиме движения прямо пропорциональны средней скорости движения; они не зависят от состояния внутренней поверхности стенок трубы, т.к. характеристика состояния стенок в формулу Пуазёйля не входит.

3. Турбулентный режим и его закономерности. Структура потока. Мгновенные и осреднённые скорости. Пульсация мгновенной скорости. Распределение осреднённых скоростей по живому сечению потока. Средняя скорость и её соотношение с максимальной скоростью в круглой трубе.

Местная мгновенная скорость u – скорость в данной точке в данный момент времени.

Местная осреднённая скорость ū – средняя скорость в данной точке.

Изменения скорости на графике кажутся беспорядочными. Но можно отметить, что осреднённое за достаточно длинный промежуток времени Т значение скорости сохраняется постоянным. Это значит, что скорость непрерывно пульсирует около некоторого среднего (осреднённого во времени) значения.

Пульсационная скорость (пульсация) u’ – разница между местной мгновенной и осреднённой скоростями: .

В турбулентном потоке вместо поля мгновенных можно рассматривать после осреднённых скоростей. Только имея в виду осреднённые скорости, можно говорить об установившемся турбулентном движении. Благодаря этому можно уловить некоторую общую закономерность несмотря на видимую беспорядочность движения отдельных частиц.

Распределение скоростей. Характер этого распределения может сильно изменяться в зависимости от диаметра трубы, скорости движения, вязкости жидкости и шероховатости стенок труб. Рассмотрим плоское равномерное турбулентное движение вдоль твёрдой границы в системе координат xyz. Направление оси OX совпадает с направлением линий тока осреднённого движения, которые представляют собой параллельные прямы. Тогда:  z – расстояние данной точки от стенки до нормали.

Касательное напряжение в турбулентном потоке:

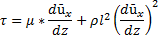
Если поток сильно турбулизирован, то первое слагаемое пренебрежимо мало, и тогда:

Для вывода закона распределения скоростей введём предположения относительно длины пути перемешивания l. Для определения длины пути перемешивания существует несколько формул, но наиболее простая из них – формула Прандтля, согласно по которой в безграничном потоке, движущемся вдоль плоской твёрдой стенки, l=κz, где κ - коэффициент (постоянная Кáрмана).

В турбулентных потоках вблизи стенки трубы можно принять l=0,4z, κ=0,4. Примем следующее:

Согласно формуле выше, l приобретает наибольшее значение при l=2/3*r₀, а на стенке и оси трубы длина перемешивания l=0. Коэффициент Кармана зависит от числа Рейнольдса и он изменяется при переходе от одних точек к другим в пределах живого сечения.

Для зоны живого сечения, в которой можно вследствие интенсивного перемешивания пренебречь чисто вязкостными напряжениями, т. е. в турбулентном ядре, можно принимать:

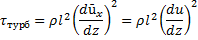
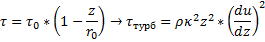
Можно принять постоянную Кармана как не зависимую от месторасположения рассматриваемой точки по отношению к стенке трубы, т. е. от z. Тогда, вынеся u_*/κ за знак интеграла, получим:

Т. е. формула представляет собой логарифмический закон распределения по живому сечению осреднённых скоростей в турбулентном потоке.

Средняя скорость и её соотношение с максимальной скоростью в круглой трубе. Так, максимальная осреднённая скорость определена формулой:

λ – коэффициент гидравлического трения.

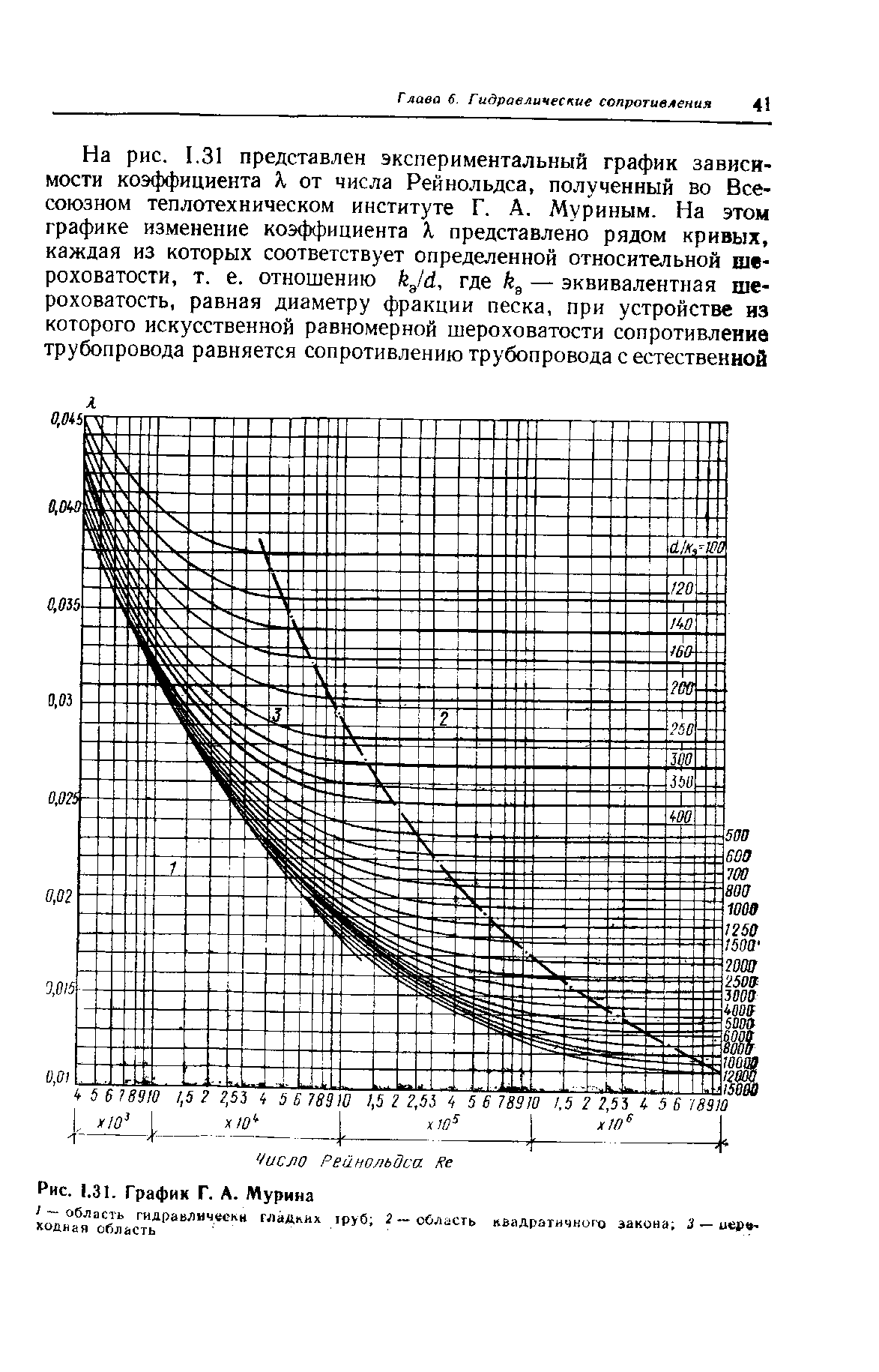
4. Потери напора при турбулентном установившемся равномерном движении. Понятия гидравлически гладких и шероховатых стенок. Эквивалентная шероховатость. Зоны сопротивления и определение их границ. Графики Никурадзе и Мурина.

Как и распределение скоростей, потери напора при турбулентном режиме движения жидкости в трубопроводе сильно зависит от диаметра трубы, скорости, вязкости и шероховатости. Шероховатость же при этом определяется рядом факторов: материалом стенок, характером механической обработки внутренней поверхности трубы, наличием или отсутствием ржавчины, коррозии, отложения солей в трубе.

Для грубой количественной оценки шероховатости вводится понятие абсолютной шероховатости Δ, мм – средней высоты выступов шероховатости.

Относительная шероховатость Δ/d, б/р – отношение абсолютной шероховатости к диаметру трубы.

Вполне шероховатые стенки – трубы, в которых коэффициент гидравлического трения λ не зависит от относительной шероховатости.

Гидравлически гладкие трубы – трубы, в которых коэффициент λ не зависит от шероховатости стенок, а только от числа Рейнольдса.

Эквивалентная шероховатость k_э – шероховатость, соответствующая средней высоте при естественной шероховатости.

Зоны сопротивления:

I – зона гладкого трения (гладких труб): потери напора обусловлены силами вязкости (силами трения между частицами).

Формула Блазиуса:

II – переходная зона: потери напора обусловлены силами трения как между самими частицами, так и между частицами и границей шероховатой поверхности.

Формула А. Д. Альтшуля:

III – квадратичная зона (вполне шероховатых труб): потери напора обусловлены силами трения на границе шероховатой поверхности.

Формула Б. Л. Шифринсона:

Установление зоны сопротивления в турбулентной зоне:

График А. И. Никурадзе: I – зона гладкого трения; II – переходная зона; III – зона вполне шероховатых труб.

 

 

График Г. А. Мурина: 1 – зона гладкого трения; 2 – зона вполне шероховатых труб; 3 – переходная зона.

 

 

5.

5. Движение жидкости в некруглых трубах. Особенности течения и расчёт потерь напора. Влияние формы сечения на потери напора.

Для транспортировки капельных жидкостей и газов в ряде случаев используются трубопроводы некругового сечения (в вентиляции, охлаждающих устройствах и пр.). В таких трубах возникают т. н. вторичные течения, которые легко можно наблюдать с помощью подкрашивания потока (опыт Рейнольдса). На рис. Показаны линии равных скоростей в турбулентных потоках треугольного сечения.

Вторичные течения происходят в плоскости поперечного сечения трубы: частицы жидкости движутся при этом из центральных районов трубы по направлению к углам. Накладываясь на продольное движение, вторичные течения непрерывно переносят количество движения по направлению к углам, в результате чего в угловых участках наблюдаются сравнительно высокие продольные скорости.

Потери на трение при турбулентном движении жидкости в трубе с поперечным сечением некруговой формы можно рассчитать по формуле Дарси-Вейсбаха, в которую вместо диаметра круглой трубы входит эквивалентный диаметр d_э.

При турбулентном движении жидкости в отличие от ламинарного основное изменение скорости происходит в пристенном слое и влияние противолежащих стенок оказывается сравнительно слабым. Этим и объясняется слабое влияние формы сечения на сопротивления при турбулентном движении. При уменьшении расстояния между стенками их взаимное влияние возрастает.