Тема 7: «Гидравлические расчёты простых трубопроводов»

1. Классификация трубопроводов. Короткие и длинные. Простые и сложные. Основные типы задач по гидравлическому расчёту простых трубопроводов.

По способам гидравлического расчёта трубопроводы подразделяют на:

· Простые трубопроводы – трубопроводы, состоящие из одной линии труб (различного диаметра), но с одним и тем же расходом по пути;

o Короткие трубопроводы – трубопроводы, у которых местные потери напора соизмеримы с потерями напора по длине (от 5 до 10% h_l); по опытам длина короткого трубопровода составляет до 50 м;

o Длинные трубопроводы – трубопроводы, у которых местные потери напора значительно меньше потерь напора по длине (менее 5 до 10% h_l); по опытам длина длинного трубопровода составляет более 50 м;

· Сложные трубопроводы – все остальные.

Существует три типа задач по расчёту коротких трубопроводов:

1) При известных параметрах: диаметре трубопровода, его длине, шероховатости – установить, какой необходимо создать напор для пропуска заданного расхода (прямая задача):

2) При тех же известных параметрах установить величину расхода жидкости при заданном напоре (обратная задача):

3) При заданных расходе, напоре, длине трубопровода и шероховатости определить, какой необходимо задать диаметр трубовпровода:

2. Применение уравнений Бернулли для расчёта коротких трубопроводов при решении задач 1-го, 2-го и 3-го типов. Построение пьезометрических линий.

Расчётные схемы: а) при истечении в атмосферу; б) при истечении под уровень:

Расчёт для схемы а):

I. Прямая задача.

1) Уравнение Бернулли:

2) Назначаем живые сечения 1-1 и 2-2 по урезу воды и в горизонтальном трубопроводе соответственно и сечение x-x, проходящее по оси трубопровода.

3)

 

4)

5)

6)

7)

8)

9) Находим λ.

10) См. п. 4 ->находим H.

II. Обратная задача.

1)-4) повторяются.

6) λ задаётся по квадратичной зоне сопротивлений:

7) Определяется v по формуле из п. 5.

8) Уточнение решения.

9)

10)

11) λ.

12) v.

13) Расход жидкости находим по формуле: .

III. 

1)-4) повторяются.

6)

7) Задаётся произвольное значение  

8) Сравнить Q₁ и Q (заданное).

9) Повторить пп. 7) и 8), если .

Расчёт для схемы б):

I. Прямая задача.

1) и 2) повторяются.

3)

6)

9) Находим λ.

10) См. п. 4 ->находим H.

II. Обратная задача.

1)-4) повторяются.

6) λ задаётся по квадратичной зоне сопротивлений:

7) Определяется v по формуле из п. 5.

8) Уточнение решения.

11) λ.

12) v.

13) Расход жидкости находим по формуле: .

III. 

1)-4) повторяются.

6)

7) Задаётся произвольное значение  

8) Сравнить Q₁ и Q (заданное).

9) Повторить пп. 7) и 8), если .

3. Особые случаи коротких напорных трубопроводов. Расчёт сифонов и всасывающих линий насосов.

Всасывающий трубопровод – гидравлически короткий трубопровод, в котором при расчёте должна быть учтены как потери по длине, так и каждая из местных потерь напора. В таком трубопроводе вследствие работы центробежного насоса на входе в него (сечение 2-2) возникает разрежение (вакуум), жидкость течёт по трубопроводу к насосу.

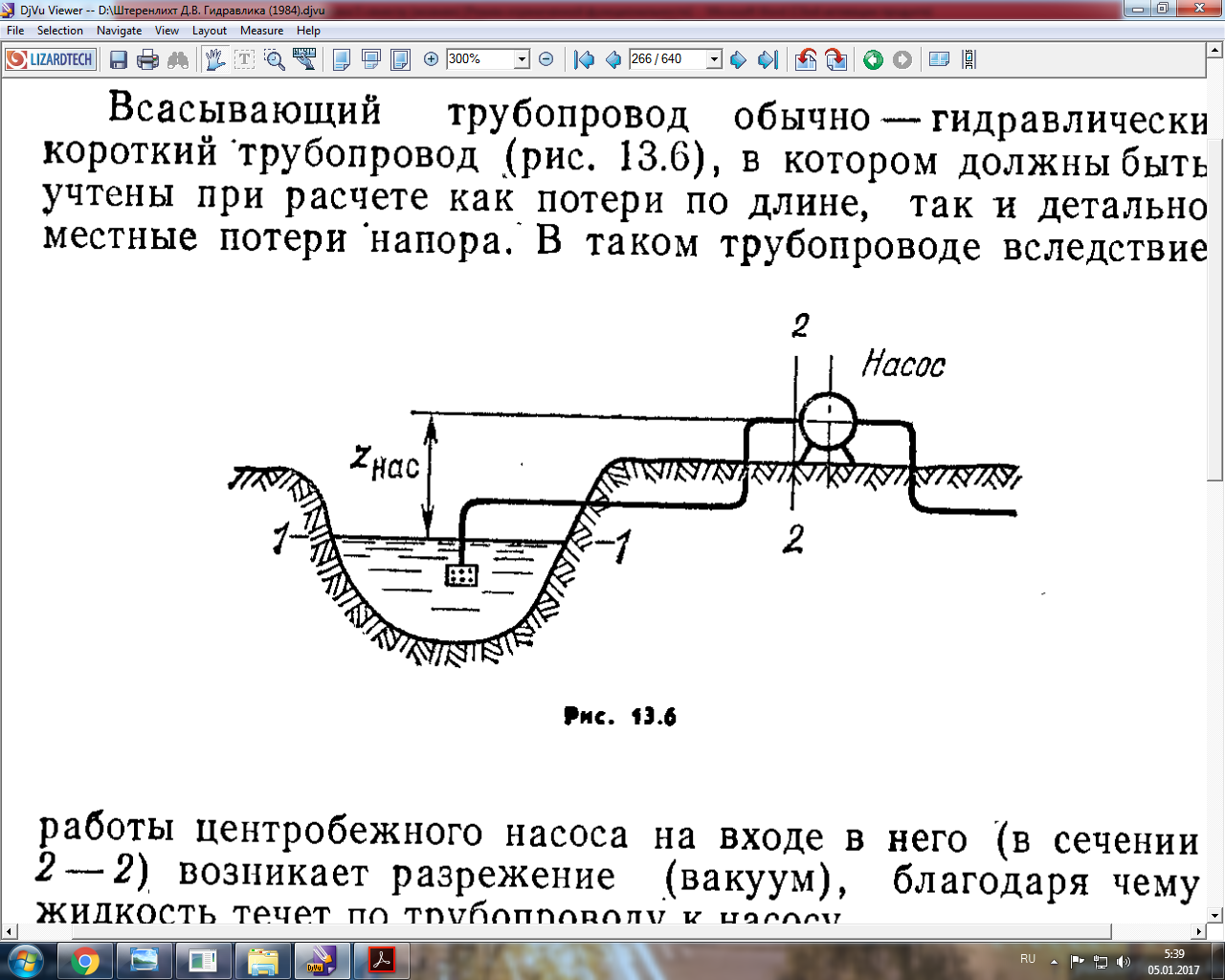Цель расчёта – определение высоты установки насоса z_нас или вакууметрической высоты во всасывающем патрубке центробежного насоса.

Сечение 1-1 – выбрано на поверхности воды в водоёме; 2-2 - непосредственно перед входом в насос во всасывающем патрубке. Плоскость сравнения совмещена с сечением 1-1. Известен расход, подаваемый насосом. Зная Q и выбрав значение v, найдём:

Приняв ближайший стандартный диаметр трубопровода, вновь вычисляют среднюю скорость в трубопроводе и вводят её в расчёт.

Рассмотрим горизонтальный насос; уравнение Бернулли имеет вид:

Высота установки насоса (геометрическая высота всасывания) при α=1:

 – сумма коэффициентов сопротивления;  – коэффициент Кориолиса.

Геометрическую высоту всасывания для горизонтального насоса определяют от уровня в водоёме до оси насоса.

Вакууметрическая высота всасывания:

Тогда:

4. Длинные трубопроводы. Формулы Шези для равномерного движения. Обобщённые гидравлические характеристики: расходная характеристика, удельное сопротивление, сопротивление трубопроводов. Модуль расхода. Потери напора с использованием обобщённых показателей.

При расчёте длинных трубопроводов скоростным напором и местными потерями пренебрегают.

Из формулы Дарси-Вейсбаха, определяющей потери напора для некруглых сечений:

Выразим потери напора через гидравлический уклон:

Формула Дарси-Вейсбаха принимает вид:

Решая уравнение формулы Шези относительно H, имеем:

Расход жидкости при равномерном движении:

Объединив параметры, зависящие от размеров (диаметра) трубы, представим их в виде т. н. расходной характеристики:

Расходная характеристика К представляет собой расход в данной трубе при гидравлическом уклоне, равном 1. Тогда:

При равномерном движении гидравлический и пьезометрический уклоны равны. Пренебрегая скоростным напором, получили, что линия удельной энергии и пьезометрическая линия совпадают. При этом расход Q и расходная характеристика К должны быть выражены в одних и тех же единицах.

Величина А – удельное сопротивление трубопровода.

В квадратичной зоне:

В неквадратичной зоне: