Пусть АВ – дуга кусочно-гладкой пространственной кривой, в каждой точке которой определена непрерывная функция f(x,y,z). Разбивая дугу на части ∆l i и выбирая в каждой части произвольную точку Mi(xi,yi,zi), вычислим значение f(Mi). Умножим это значение на длину элементарной дуги ∆li. Сложим все произведения, и найдем предел этой суммы при условии, что наибольшая из элементарных дуг max ∆li→0, а их число n→∞.
lim  f(x,y,z)dl (5.1)
f(x,y,z)dl (5.1)
max∆li→0
При непрерывности функции f(x,y,z) на дуге АВ этот предел существует и не зависит от способа разбиения дуги на части. Этот предел называется криволинейным интегралом I рода. Физическая интерпретация криволинейного интеграла первого рода (5.1) - масса кривой АВ. Вычисление криволинейного интеграла I рода сводится к вычислению определенного интеграла.
Если кривая АВ задана параметрическими уравнениями: x=X(t), y=Y(t),z=Z(t), где tА≤ t ≤ tB, то
 f(x,y,z)dl=
f(x,y,z)dl=  ·
·  dt.
dt.
Если кривая АВ задана на плоскости уравнением y=f(x) при a≤x≤b, то
 f(x,y)dl=
f(x,y)dl=  ·
·  dx.
dx.
5.1. Задачи на механические приложения криволинейного интеграла.
С помощью криволинейного интеграла I рода можно вычислить:
а) массу кривой
m=  , где
, где  - плотность
- плотность
б) статические моменты относительно координатных осей для плоской дуги
Mx = 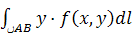 My=
My= 
в) статические моменты относительно координатных плоскостей для пространственной дуги
Mxoy=  Myoz=
Myoz= 
Mxoz= 
г) моменты инерции относительно координатных осей плоской дуги
Jx=  Jy=
Jy= 
д) координаты центра тяжести
xc= 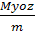 yc=
yc=  zc=
zc= 
Пример: вычислить интеграл
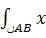 2 ydl, где ﮞ АВ – часть окружности
2 ydl, где ﮞ АВ – часть окружности  +
+  =
=  , лежащая в первой четверти.
, лежащая в первой четверти.
Тогда y=  . Найдем дифференциал дуги dl=
. Найдем дифференциал дуги dl=  dx
dx
y′=-  ;
;  =
=  ; 1 +
; 1 +  1 +
1 +  =
= 
Тогда dl=  dx
dx
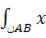 2ydl=
2ydl=  dx=R
dx=R 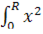 dx=
dx= 
Пример: вычислить  dl, где АВ - дуга кубической параболы y=x3 от точки (1;1) до точки (2;8)
dl, где АВ - дуга кубической параболы y=x3 от точки (1;1) до точки (2;8)
Найдем дифференциал дуги dl=  dx
dx
y′=3x2;  9x4;
9x4;  9x4;
9x4;
Тогда dl = 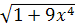 dx
dx
 d l=
d l= 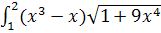 dx =
dx =  dx-
dx-  =J1-J2
=J1-J2
J1= 
 dt
dt
=  ·
· 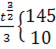 =
=  ·(
·(  -
-  )
)
J2= 
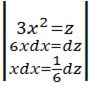 =
= 
= 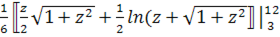
J1-J2=  ·(
·(  -
-  )-
)- 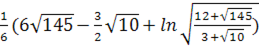
Пример: найти массу одной арки циклоиды, считая плотность постоянной, равной единице.
x =a(t-  ); y=a(1-
); y=a(1-  ); 0≤t≤2π
); 0≤t≤2π
Найдем дифференциал дуги
dl= 
 =a(1-
=a(1-  );
);  =a
=a  ;
;
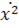 +
+  =a2(1+2
=a2(1+2  +
+  +
+  = a2(1+2
= a2(1+2  +1)=
+1)=
a2(2+2  )=2 a2(1+
)=2 a2(1+  )=4 a2
)=4 a2 
Тогда dl=2a  dt
dt
m=  =-4a
=-4a  =-4a(-1-1)=8a
=-4a(-1-1)=8a
Пример: найти массу дуги однородной пространственной кривой
 (a>0)
(a>0)
от точки О(0,0,0) до точки А(x0, y0, z0).
Если в задаче сказано, что дуга однородная, принимаем плотность f(x,y,z)=const= 1.
Найдем массу дуги по формуле m=  при dl=
при dl= 

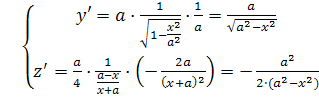
dl= 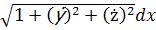 =
=  dx=
dx= 
m=  =
=  ·
· 
=  =
=  =
= 
Пример: найти статический момент относительно плоскости XOY части
однородной конической винтовой линии.
x =t ∙cos t, y= t∙ sin t, z=t при 0≤t≤t0
Mxoy= 
dl= 
 = (tcos(t))′=t′cos(t)+t(cos(t))′=cos(t)-tsin(t)
= (tcos(t))′=t′cos(t)+t(cos(t))′=cos(t)-tsin(t)
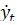 =(tsin(t))′=t′sin(t)+t(sin(t))′=sin(t)+tcos(t)
=(tsin(t))′=t′sin(t)+t(sin(t))′=sin(t)+tcos(t)

dl= 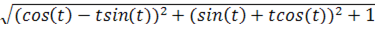 dt=
dt=
=  =
=
=  dt=
dt=  dt
dt
f(x,y,z)=const=1
Mxoy=  =
=  dt=
dt=  =
=
=  =
=  dx=
dx= 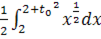 =
=  (
(  )=
)=  (
(  -
-  )
)
Пример: найти центр тяжести однородной дуги.
(-∞< t ≤ 0) 
Примем плотность f(x,y,z)=const= 1
m=  dl
dl
dl= 
ẋ=  -
- 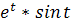 =
= 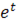 (cost-sint)
(cost-sint)
ẏ=  +
+  =
= 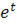 (sint+cost)
(sint+cost)
ż= 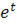
dl=  dt=
dt= 
= 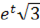 dt
dt
m=  =
=  =
=  (
(  -
-  )=
)= 
Myoz= 
Myoz=  *costdt=
*costdt=  *costdt=
*costdt=  (
(  (sint+2cost)
(sint+2cost)  =
=
=  *
*  *2=0.4
*2=0.4 
При вычислении интеграла используем формулу “интегрирования по частям”
 *costdt
*costdt  dt
dt  =
=
=  *cost-4
*cost-4 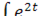 *costdt
*costdt
5 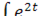 *costdt=
*costdt=  *cost
*cost
 *costdt=
*costdt= 
Mzox= 
Mzox=  *sintdt=
*sintdt=  (
( 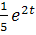 (cost-2sint)
(cost-2sint) 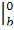 =
=
=  *( -
*( -  )*1=- 0.2
)*1=- 0.2 
При вычислении интеграла используем формулу “интегрирования по частям”
 *sintdt
*sintdt  =-
=- 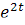 *cost 2
*cost 2 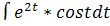 +
+  =
=
=-  *cost+2
*cost+2  *sint- 4
*sint- 4  *costdt
*costdt
5  =-
=- 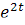 *sint+2
*sint+2  *cost
*cost
 =-
=- 
Mxoy= 
Mxoy=  dt=
dt=  =
= 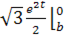 =
=  *
*  =0.5
=0.5 
Координаты центра тяжести:
xц.т.=  =
=  =0.4
=0.4
yц.т.=  =
=  =-0.2
=-0.2
zц.т.= 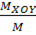 =
=  =0.5
=0.5
6. Поверхностный интеграл первого рода
 Пусть S – поверхность в трёхмерном пространстве Оxyz, а F(x,y,z) непрерывная функция, определённая в точках этой поверхности. Поверхность S сетью линий разобьём на n участков ΔS1, ΔS2,...., ΔSi,..., ΔSn, не имеющих общих внутренних точек (рис.6.1). Площади "элементарных" участков обозначим теми же буквами Si(i = 1,...,n), а наибольший из диаметров этих участков через λ. На каждом "элементарном" участке ΔSi произвольным образом выберем по точке Mi(xi,yi,zi) (i = 1,...,n) и составим сумму
Пусть S – поверхность в трёхмерном пространстве Оxyz, а F(x,y,z) непрерывная функция, определённая в точках этой поверхности. Поверхность S сетью линий разобьём на n участков ΔS1, ΔS2,...., ΔSi,..., ΔSn, не имеющих общих внутренних точек (рис.6.1). Площади "элементарных" участков обозначим теми же буквами Si(i = 1,...,n), а наибольший из диаметров этих участков через λ. На каждом "элементарном" участке ΔSi произвольным образом выберем по точке Mi(xi,yi,zi) (i = 1,...,n) и составим сумму

которая называется интегральной суммой для функции F(x,y,z) по поверхности S.
Если существует конечный предел

не зависящий от способа разбиения поверхности S на "элементарные" участки ΔSi и от выбора точек Mi  ΔSi(i=1,....n), то он называется поверхностным интегралом первого рода от функции F(x,y,z) по поверхности S и обозначается
ΔSi(i=1,....n), то он называется поверхностным интегралом первого рода от функции F(x,y,z) по поверхности S и обозначается

Если поверхность S задана уравнением z= f(x,y), где функция f(x,y) и её частные производные f'x(x,y) и f'y(x,y) непрерывны в замкнутой области координатной плоскости Oху, а функция F(x,y,z) непрерывна на S, то интеграл

существует.
Вычисление поверхностных интегралов первого рода обычно производится путём их сведения к двойным интегралам. Пусть выполнены все условия, приведенные выше, тогда, обозначив проекцию ΔSi (и площадь проекции) на плоскость Oxy через ΔDi, по теореме о среднем будем иметь:

где (xi, yi)  ΔDi, а, следовательно,
ΔDi, а, следовательно,

при данном выборе точек Mi. Но сумма, стоящая справа, в последнем интеграле есть интегральная сумма для функции

Переходя к пределу, получаем:

Свойства поверхностного интеграла первого рода
1. Если положить F(x,y,z)=1, то интеграл будет численно равен площади поверхности S.
2.Постоянный множитель можно вынести за знак интеграла.
3.Интеграл от алгебраической суммы функций равен сумме интегралов от слагаемых.
4.Если область S состоит из 2-х частей, описываемых разными уравнениями, то
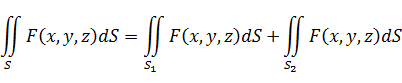
5.Если F(x,y,z)≥ φ (x,y,z) то

6.

6.2. Задачи на механические приложения поверхностного интеграла 1-ого рода.
1.Если F(x,y,z) - плотность вещества, то масса поверхности S

2.Если F(x,y,z)=1, то интеграл численно равен площади поверхности S.
3.Статистические моменты относительно координатных плоскостей

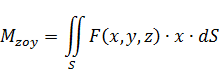

4.Моменты инерции относительно координатных осей



5.Моменты инерции относительно координатных плоскостей

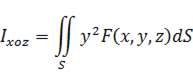

6.Координаты центра масс


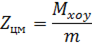
Пример: вычислить поверхностный интеграл

 где S - поверхность конуса
где S - поверхность конуса

при 1≤ z ≤2 (рис.6.2)
Очевидно, что поверхность S проектируется на плоскость Oxy в кольцо D: 1 ≤x2+y2 ≤2
В области D функция

и её производные
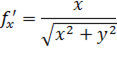
и

Следовательно,


Пример: вычислить поверхностный интеграл I рода.

где S – часть плоскости x+y+z=1, лежащая в I октанте.
z=1-x-y, zx’=-1; zy’=-1

 рис.6.3.
рис.6.3.



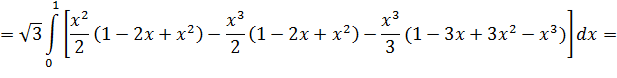



Пример: найти массу поверхности полусферы

если в каждой её точке поверхностная плоскость вещества пропорциональна квадрату расстояния этой точки от оси Oz.
Имеем

и, следовательно,




x2+y2≤4 – переходим в полярную систему координат



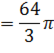
Масса поверхности полусферы равна  .
.
Пример: найти моменты инерции однородной треугольной пластины x+y+z=1 при (x≥0;y≥0;z≥0) относительно координатных плоскостей.
Моменты инерции относительно координатных плоскостей вычисляются по формулам:
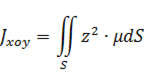
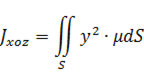

где µ - плотность пластины (у однородной пластины µ=1).




рис.6.4.






Моменты инерции равны между собой, т.к. пластина расположена симметрично относительно осей координат в первом октанте.
Таблица производных
(u+v-w)′=u′+v′+w′ c′=0 x′=1
(u·v)′= u′v + v′u
(c·u)′= c·u′
 ′=
′= 
(un)′x= n·un-1·u′x (xn)′= n·xn-1
(  )′=
)′=  (
(  )′=
)′= 
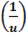 ′= -
′= - 
 ′= -
′= - 
(au)′x= au·lna·u′ (ax)′= ax·lna
(eu)′= eu·u′ (ex)′= ex
(lnu)′=  (lnx)′=
(lnx)′= 
(logau)′=  (logax)′=
(logax)′= 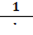
(lgu)′=  (lgx)′=
(lgx)′= 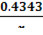
( 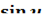 )′x=
)′x=  ·u′ (
·u′ (  )′=
)′= 
(  ′x=-
′x=-  ·u′ (
·u′ ( 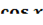 )′= -
)′= - 
(tgu)′=  (tgx)′=
(tgx)′= 
(ctgu)′= -  (ctgx)′= -
(ctgx)′= - 
(arccosu)′x= -  (arccos x)′= -
(arccos x)′= - 
(arcsinu)′x=  (arcsin x)′=
(arcsin x)′= 
(arctgu)′x=  (arctgx)′=
(arctgx)′= 
(arcctgu)′x=  (arcctgx)′= -
(arcctgx)′= - 
| № п\п | Вид интеграла | Метод интегрирования |
| 1 |  | Подстановка φ(x)=t |
| 2 |  | Интегрирование по частям  =f(x)φ(x)- =f(x)φ(x)-  Метод интегрирования по частям применяется, например, к интегралам вида Метод интегрирования по частям применяется, например, к интегралам вида 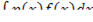 , где p(x) – многочлен, eax;cos ax;sin ax;lnx;arctg x;arcsin x и т.п.,а также к интегралам от произведений показательной функции на косинус или синус. , где p(x) – многочлен, eax;cos ax;sin ax;lnx;arctg x;arcsin x и т.п.,а также к интегралам от произведений показательной функции на косинус или синус. |
| 3 |  (x)dx (x)dx | Сводится к интегрированию произведения  (x)φ(x) с помощью формулы кратного интегрирования по частям: (x)φ(x) с помощью формулы кратного интегрирования по частям:  (x)dx= =f(x) (x)dx= =f(x)  -f′(x) -f′(x)  + +f′′(x) + +f′′(x)  (x)-… …+(-1)n-1f(n-1)(x)φ(x)+ +(-1)n (x)-… …+(-1)n-1f(n-1)(x)φ(x)+ +(-1)n  |
| 4 |  pn(x)dx pn(x)dx | Применяя формулу кратного интегрирования по частям, получим  pn(x)dx= pn(x)dx=  +C +C |
| 5 |  P3-4q<0 P3-4q<0 | Подстановка x+  =t =t |
| № п\п | Вид интеграла | Метод интегрирования |
| 6 | In=  | Применение рекуррентной формулы In=  + +  In-1 In-1 |
| 7 |  dx, где dx, где  -правильная рациональная дробь, Q(x)=(x-x1)′(x-x2 -правильная рациональная дробь, Q(x)=(x-x1)′(x-x2  ... …( ... …( +px+q +px+q  … … | Подынтегральную дробь представляют в виде суммы простейших дробей  = =  + + 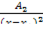 +…+ +…+  + + + +  + +  +… +…  +…+ +…+ 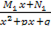 + + 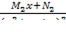 +…+ +…+  +… +… |
| 8 |  ,…, ,…, 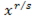 )dx, где R-рациональная функция своих аргументов )dx, где R-рациональная функция своих аргументов | Приводится к интегралу от рациональной дроби подстановкой x=  , где k – общий знаменатель дробей , где k – общий знаменатель дробей  ,…, ,…,  |
| 9 | 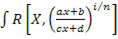 dx dx | Сводится к интегралу от рациональной дроби подстановкой  = =  |
| 10 |  dx dx | Подстановкой x +  =t интеграл приводится к сумме двух интегралов =t интеграл приводится к сумме двух интегралов  dx=M1 dx=M1 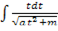 + +N1 + +N1  Первый интеграл сводится к интегралу от степенной функции, а второй интеграл – табличный. Первый интеграл сводится к интегралу от степенной функции, а второй интеграл – табличный. |
| № п\п | Вид интеграла | Метод интегрирования |
| 11 |  )dx, где R –рациональная функция от x и )dx, где R –рациональная функция от x и  | Приводится к интегралу от рациональной дроби подстановками Эйлера  = t±x = t±x  (a>0), (a>0),  =tx± =tx±  (c>0) (c>0)  =t(x- =t(x-  ) (4ac- ) (4ac-  ), где ), где  - корень трехчлена - корень трехчлена  Для вычисления указанного интеграла применяются также тригонометрические подстановки: x+ Для вычисления указанного интеграла применяются также тригонометрические подстановки: x+  = =  (a<0, 4ac-b2<0) x+ (a<0, 4ac-b2<0) x+  = = 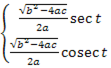 (a>0, 4ac-b2<0) x+ (a>0, 4ac-b2<0) x+  = =  (a>0, 4ac-b2>0) (a>0, 4ac-b2>0) |
| 12 |  dx где dx где  - многочлен степени n - многочлен степени n | Записываем равенство  =Qn-1(x) =Qn-1(x)  + +k + +k  , где Qn-1(x)- многочлен степени n-1 Дифференцируя обе части этого равенства и умножая на , где Qn-1(x)- многочлен степени n-1 Дифференцируя обе части этого равенства и умножая на  , получим тождество , получим тождество  )= Qn-1(x)( )= Qn-1(x)( + + + +  Qn-1(x)(2ax+b)+k Которое дает систему n+1 линейных уравненений для определения коэффициентов многочлена Qn-1(x) и множителя k. Интеграл же Qn-1(x)(2ax+b)+k Которое дает систему n+1 линейных уравненений для определения коэффициентов многочлена Qn-1(x) и множителя k. Интеграл же  берется методом, указанным в п.10 (M=0;N=1) берется методом, указанным в п.10 (M=0;N=1) |
| № п\п | Вид интеграла | Метод интегрирования |
| 13 |  | Этот интеграл приводится подстановкой  = =  к интегралу рассмотренному выше. к интегралу рассмотренному выше. |
| 14 |  (a+b (a+b  )pdx, Где m,n,p-рациональные числа (интеграл от биноминального дифференциала) )pdx, Где m,n,p-рациональные числа (интеграл от биноминального дифференциала) | Интеграл от биноминального дифферециала выражается через элементарные функции только при выполнении одного из следующих условий: 1) если p-целое число 2) если  – целое число 3) если – целое число 3) если  + p – целое число 1-й случай а)если p-целое положительное число,то нужно раскрыть скобки (a+b + p – целое число 1-й случай а)если p-целое положительное число,то нужно раскрыть скобки (a+b  )p по биному Ньютона и вычслить интегралы от степеней; б)если p- целое отрицательное число, то подстановка x = )p по биному Ньютона и вычслить интегралы от степеней; б)если p- целое отрицательное число, то подстановка x =  , где k – общий знаменатель дробей m и n, приводит к интегралу от рациональной дроби; 2-й случай если , где k – общий знаменатель дробей m и n, приводит к интегралу от рациональной дроби; 2-й случай если  - целое число, то применяется подстановка a+b - целое число, то применяется подстановка a+b  =tk, где k – знаменатель дроби p; 3-й случай если =tk, где k – знаменатель дроби p; 3-й случай если  - целое число, то применяется подстановка a+b - целое число, то применяется подстановка a+b  = =  tk, где k – знаменатель дроби p; tk, где k – знаменатель дроби p; |
| 15 |  | Универсальная подстановка tg  =t Если R(- =t Если R(-  = - R( = - R( , то подстановка , то подстановка 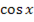 =t. Если R( =t. Если R( ,то подстановка ,то подстановка  =t. Если R( =t. Если R( ,то подстановка ,то подстановка  =t. =t. |
| № п\п | Вид интеграла | Метод интегрирования |
| 16 | R(sh x, ch x)dx | Применяется подстановка th  =t. При этом sh x= =t. При этом sh x=  ;ch x= ;ch x=  ;dx= ;dx=  |
| 17 |    | Необходимо преобразовать произведение тригонометрических функций в сумму или разность, пользуясь одной из следующих формул:  = = 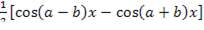  = = = =   = = = =  |
| 18 |  , где m и n – целые числа , где m и n – целые числа | Если m-нечетное положительное, то подстановка 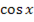 =t. Если n-нечетное положительное, то подстановка =t. Если n-нечетное положительное, то подстановка  =t. Если m+n-четное отрицательное, то подстановка tgx=t. Если m и n –четные неотрицательные, то применяют формулы: =t. Если m+n-четное отрицательное, то подстановка tgx=t. Если m и n –четные неотрицательные, то применяют формулы:  = =  ; ;  = =  |
| 19 |  , (0<x< , (0<x<  ) p и q- рациональные числа ) p и q- рациональные числа | Подстановкой  =t приводится к интегралу от биноминального дифференциала =t приводится к интегралу от биноминального дифференциала 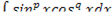 =tp(1-t2 =tp(1-t2  dt dt |
| 20 |  )dx )dx | Постановка  преобразуется в интеграл от рациональной функции. преобразуется в интеграл от рациональной функции. |
Варианты заданий на несобственные интегралы и ФМП
Вариант № 1
 2020-04-12
2020-04-12 2675
2675
