Начертить область, на которую распространен двойной интеграл, изменить порядок интегрирования и записать интеграл в полярной системе координат

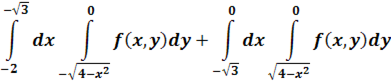
2. В тройном интеграле 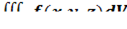, где V – область, ограниченная данными поверхностями, расставить пределы интегрирования в декартовой, цилиндрической и сферической системах координат.

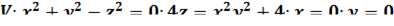
д ля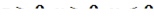  

3. Найти площадь фигуры, ограниченной линиями:

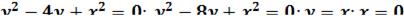
4. Найти координаты центра тяжести однородной дуги:

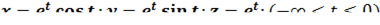
Вариант № 3

Начертить область, на которую распространен двойной интеграл, изменить порядок интегрирования и записать интеграл в полярной системе координат.

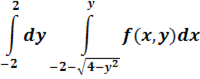
2. В тройном интеграле 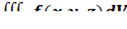, где V – область, ограниченная данными поверхностями, расставить пределы интегрирования в декартовой, цилиндрической и сферической системах координат.

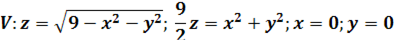
для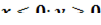

3. Найти объем тела, заданного поверхностями:

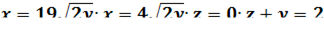
4. Найти массу дуги однородной пространственной кривой:

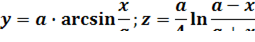
от точки  до точки

Вариант № 4

Начертить область, на которую распространен двойной интеграл, изменить порядок интегрирования и записать интеграл в полярной системе координат.

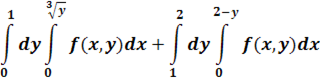
2. В тройном интеграле 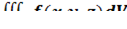, где V – область, ограниченная данными поверхностями, расставить пределы интегрирования в декартовой, цилиндрической и сферической системах координат.

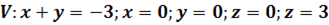
3. Найти объем тела, ограниченного поверхностями:

 

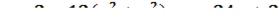
4. Найти массу полусферы 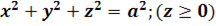 плотность которой в каждой её точке  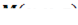равна  

Вариант № 5

Начертить область, на которую распространен двойной интеграл, изменить порядок интегрирования и записать интеграл в полярной системе координат.

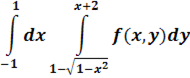
2. В тройном интеграле 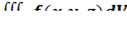, где V – область, ограниченная данными поверхностями, расставить пределы интегрирования в декартовой, цилиндрической и сферической системах координат.

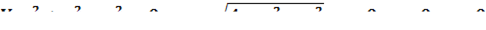
для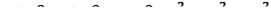

3. Найти объем тела, ограниченного поверхностями:

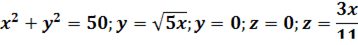
4. Найти статические моменты однородной треугольной пластинки 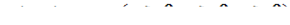 относительно координатных плоскостей.

Вариант № 6