z= 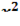 +xy+
+xy+ 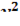 +x-y+1
+x-y+1
Вариант № 10
Вычислить несобственный интеграл или установить его расходимость
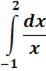
2. Найти производную 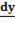 из равенства
из равенства 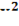 +
+ 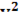 +
+ 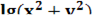 =
= 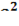
3. Написать уравнения касательной плоскости и нормали к поверхности 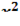 -
- 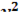 +
+ 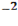 =4 в точке M (1;1;-2)
=4 в точке M (1;1;-2)
Исследовать функцию на экстремум
f(x,y,z)=4xy+4yz-5 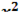 -6
-6 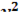 -4
-4 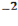 -x+6y
-x+6y
Вариант № 11
Исследовать интеграл на сходимость
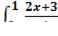 dx
dx
2. Найти 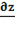 и
и 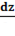 , если z=
, если z= 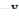 , y=arctg
, y=arctg 
3. Найти производную функции u(x,y,z)=xy+yz+zx в точке M (2;1;3)
в направлении вектора 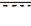 , если N (5;5;15)
, если N (5;5;15)
4. Найти уравнения касательной плоскости и нормали к поверхности:
7 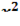 -4
-4 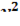 +4
+4 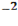 =7 в точке M(1;1;1).
=7 в точке M(1;1;1).
Вариант № 12
Вычислить интеграл или установить его расходимость
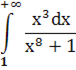
2. Найти  и
и 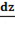 , если z=
, если z= 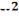 y и y=
y и y= 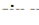
Найти уравнения касательной плоскости и нормали к поверхности
z=1+ 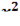 +
+ 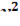 в точке M (1;1;3)
в точке M (1;1;3)
4. Исследовать функцию на экстремум f(x,y,z)=xy+yz+xz+x-y+z
Вариант № 13
Исследовать интеграл на сходимость
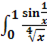 dx
dx
2. Найти 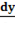 , если
, если  +
+  )=a
)=a
3. Найти производную скалярного поля u(x,y,z)=ln(  +
+ 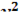 )+xyz
)+xyz
в точке M (1;-1;2) по направлению вектора 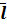 =
=  -
- 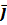 +5
+5 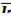
4. Найти уравнения касательной плоскости и нормали поверхности:
z= 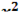 +
+ 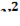 -4 в точке M (-2;1;1)
-4 в точке M (-2;1;1)
Вариант № 14
Вычислить интеграл или установить его расходимость
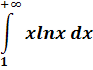
2. Найти  и
и 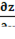 , если z=x+arctg
, если z=x+arctg 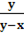
Найти точки локального экстремума функции
u(x,y)=xy+ 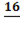 +
+ 
4. Найти уравнения касательной плоскости и нормали к поверхности:
 +
+ 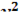 -
- 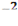 =-1 в точке M (2;2;3)
=-1 в точке M (2;2;3)
Вариант № 15
Исследовать интеграл на сходимость
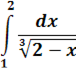
2. Найти 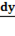 из равенства
из равенства 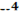 -2
-2  y+
y+ 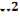 +
+ 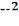 -y=0
-y=0
3. Найти уравнения касательной плоскости и нормали к поверхности:
 -4
-4 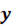 в точке M (2;1;4)
в точке M (2;1;4)
Найти производную скалярного поля
u(x,y,z)= 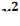 - arctg(y+z) в точке M (2;1;1) в направлении вектора
- arctg(y+z) в точке M (2;1;1) в направлении вектора
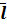 =3
=3 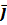 -4
-4 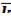
Варианты заданий на двойные и тройные интегралы
Вариант № 1
Начертить область, на которую распространен двойной интеграл, изменить порядок интегрирования и записать интеграл в полярной системе координат.
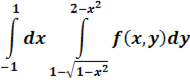
2. В тройном интеграле 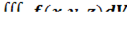 , где V – область, ограниченная данными поверхностями, расставить пределы интегрирования в декартовой, цилиндрической и сферической системах координат.
, где V – область, ограниченная данными поверхностями, расставить пределы интегрирования в декартовой, цилиндрической и сферической системах координат.
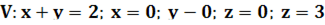
3. Найти объем тела, заданного неравенствами:
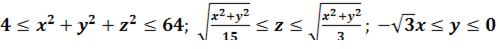
Найти моменты инерций относительно координатных осей одного витка однородной винтовой линии
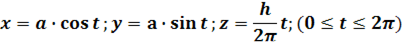
Вариант № 2
 2020-04-12
2020-04-12 188
188








