Задача 1. Снаряд массой m=20 кг выпущен вертикально вверх из зенитного орудия с начальной скоростью V0=100 м/с. найдите кинетическую энергию снаряда в момент времени t=10 с. На какой высоте кинетическая энергия равна нулю?
Решение: а). Высота h снаряда подчиняется закону h(t)=V0t- 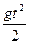 , где g – ускорение свободного падения, g≈9,8 м/с2. Следовательно, скорость снаряда в момент времени t равна V(t)=h′(t)=V0-gt.
, где g – ускорение свободного падения, g≈9,8 м/с2. Следовательно, скорость снаряда в момент времени t равна V(t)=h′(t)=V0-gt.
V(10)=100-g∙10≈100-9,8∙10=100-98=2 (м/с)
Е к= 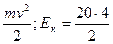 =40 (Дж)
=40 (Дж)
б). Кинетическая энергия равна нулю, когда скорость равна нулю, т.е.
V0-gt=0, откуда t= 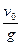 . Е к=0, если снаряд находится на высоте
. Е к=0, если снаряд находится на высоте 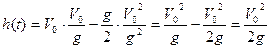 ;
; 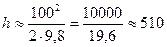 (м)
(м)
Ответ: Е к≈40 Дж, h≈510 м.
Задача 2. Высота снаряда, вылетевшего с начальной скоростью V0 под углом α к горизонту измеряется по закону h(t)=V0sinα 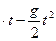 . Известно, чтоV0=500 м/с, а через 1с скорость изменения высоты снаряда была равна 24g м/с. Под каким углом к горизонту вылетел снаряд?
. Известно, чтоV0=500 м/с, а через 1с скорость изменения высоты снаряда была равна 24g м/с. Под каким углом к горизонту вылетел снаряд?
При решении взять g≈10 м/с2.
Решение: V(t)=h′(t)= 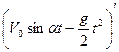 =V0sinα-gt;
=V0sinα-gt;
 V(1)=500sinα-g;
V(1)=500sinα-g;
500sinα-g=24g;
α h(t) 500sinα=25g
sinα= 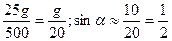
α≈300.
Ответ: снаряд вылетел под углом 300 к горизонту.
Задача 3. Осветительная ракета запускается вертикально вверх с поверхности Земли и движется по закону h(t)=80t-4t2 (h измеряется в метрах, t – в секундах). Труба, высота которой 40 м, находится в 18 м от места запуска ракеты. Найдите скорость изменения длины тени от трубы в тот момент времени, когда длина тени равна 10 м.
Решение:
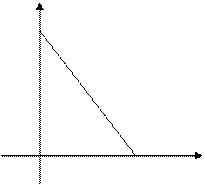  y B M C 40 18 O D A x y B M C 40 18 O D A x | Место запуска ракеты – точка О, точка D – основание трубы, С – верх трубы. Если ракета в произвольный момент времени находится в точке В, то конец тени от трубы находится в точке А. ОD=18 м, CD=40 м, ОВ=h(t), ВМ=h(t)-40 |
Длина тени от трубы равна длине отрезка AD. Обозначим AD=x(t′).
∆BMC~∆CDA. Отсюда, 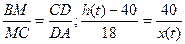 , откуда x(t)=
, откуда x(t)= 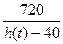 . Скорость изменения тени найдем, как производную функции x(t), используя правило дифференцирования сложной функции:
. Скорость изменения тени найдем, как производную функции x(t), используя правило дифференцирования сложной функции:  .
.
В этом выражении неизвестен момент времени t, который соответствует значению x(t)=10 (м). Так как x(t)= 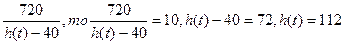 .
.
Из условия задачи имеем h(t)=80t-4t2;
112=80t-4t2; 4t2-80t+112=0.
Отсюда, t1=10-6 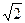 ; t2=10+6
; t2=10+6 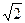 , где t1 соответствует подъему ракеты, а t2 – ее спуску.
, где t1 соответствует подъему ракеты, а t2 – ее спуску.
h′(t)=80-8t; h′(t1)=80-8(10-6 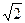 )=48
)=48 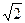
h′(t2)=80-8(10+6 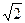 )=-48
)=-48 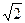
Поэтому, х′(t1)=- 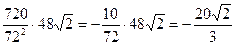 (м/с)
(м/с)
х′(t2)= 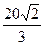 (м/с).
(м/с).
Знак „-” скорости изменения величины x(t) говорит о том, что длина тени при подъеме ракеты уменьшается, а при спуске ракеты тень от трубы увеличивается.
Ответ: x′(t)= 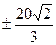 (м/с).
(м/с).
Задача 4. Из пункта А выходит мотоцикл, движущийся равноускоренно по закону S(t)= 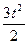 . В какой момент времени мотоцикл догонит автомашину, которая вышла из А одной минутой раньше мотоцикла и движется в том же направлении со скоростью 15 м/с? С какой скоростью мотоцикл удаляется от автомашины в момент из встречи?
. В какой момент времени мотоцикл догонит автомашину, которая вышла из А одной минутой раньше мотоцикла и движется в том же направлении со скоростью 15 м/с? С какой скоростью мотоцикл удаляется от автомашины в момент из встречи?
Решение: За 1 мин машина прошла 15·60=900 (м). Поэтому, расстояние между машиной и мотоциклом в любой момент времени t после выхода мотоцикла до момента их встречи равно S(t)= 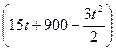 м.
м.
В момент встречи это расстояние равно нулю, т.е. имеем 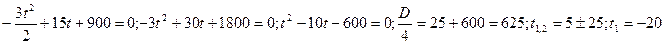 (не удовлетворяет условию задачи), t2=30 (с). Следовательно, встреча произошла через 30 с после выхода мотоцикла. Vмот.=
(не удовлетворяет условию задачи), t2=30 (с). Следовательно, встреча произошла через 30 с после выхода мотоцикла. Vмот.= 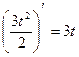 ; V(30)=3·30=90 (м/с), а скорость удаления мотоцикла равна 90м/с-15/с=75м/с.
; V(30)=3·30=90 (м/с), а скорость удаления мотоцикла равна 90м/с-15/с=75м/с.
Ответ: t=30 c, Vуд.=75 м/с.
Задача 5. Лестница длиной 5 м приставлена к стене таким образом, что верхний ее конец находится на высоте 4 м. В некоторый момент времени лестница начинает падать, при этом верхний конец приближается к поверхности земли с постоянным ускорением 2м/с2. С какой скоростью удаляется от стены нижний конец лестницы в тот момент, когда верхний конец находится на высоте 3 м?
Решение: Пусть верхний конец лестницы находится в момент времени t на высоте h(t), h(0)=4(м), а нижний конец находится на расстоянии x(t) от основания стены. Тогда высота h(t) описывается формулой h(t)=4- 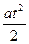 . Учитывая, что а =2 м/с2, имеем h(t)=4-t2.
. Учитывая, что а =2 м/с2, имеем h(t)=4-t2.
| 5м 4м 3м х(t) | Для нахождения момента времени t, когда h(t)=3 имеем уравнение 4-t2=3, из которого t2=4-3; t2=1, t=1 (с). По теореме Пифагора расстояние 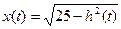 . . 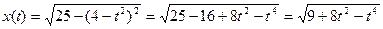 |
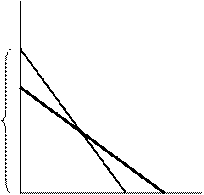 Скорость изменения расстояния V(t)=x’(t)= =
Скорость изменения расстояния V(t)=x’(t)= = 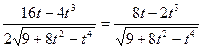 .
.
V(1)= 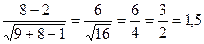 (м/с).
(м/с).
Ответ: скорость удаления нижнего конца лестницы от стены равна 1,5 м/с.
Задача 6. При нагревании круглый металлический диск расширяется, причем его радиус увеличивается равномерно со скоростью V=0,2 см/ч. Вычислите начальный радиус диска, если известно, что через 15 мин после начала нагревания скорость увеличения площади диска равна 2,02π см2/ч.
Решение: Пусть начальный радиус диска равен r. Тогда в момент времени t радиус будет равен r1=r+Vt, а площадь диска при этом будет равной S(t)=πr12=π(r+Vt)2.
Скорость увеличения площади S’(t)=2πV(r+Vt).
При t=15 мин= 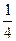 ч ч | S΄ 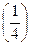 =2,02π (по условию задачи) =2,02π (по условию задачи) |
| C другой стороны | S΄ 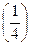 =2π·0,2 =2π·0,2 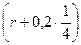 =0,4πr+0,02π =0,4πr+0,02π |
| Следовательно | 0,4πr+0,02π=2,02π 0,4πr=2π 0,4r=2 r=5 (см) |
Ответ: начальный радиус диска 5 см.
Задача 7. Паром подтягивается к берегу при помощи каната, который наматывается на ворот со скоростью 40 м/мин. Ворот находится на берегу на 10 м выше поверхности воды. Найти скорость движения парома в тот момент, когда он находится в 30 м от берега.
Решение: Пусть паром находится в точке В, а ворот – в точке А и x(t) – расстояние от парома до берега, АВ=S(t).
По теореме Пифагора: AB= 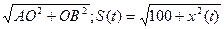
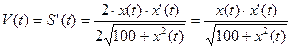 - скорость наматывания каната.
- скорость наматывания каната.
A 10м 30м О х(t) B x 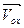 | По условию задачи S’(t)=-40, т.к. расстояние АВ сокращается. По условию x(t)=30, тогда S’(t)= 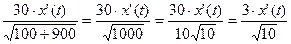 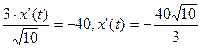 (м/мин). (м/мин). |
Значит, скорость движения парома в 30 м от берега равна 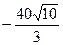 м/мин, знак „-” означает, что паром приближается к берегу, т.е. x(t) уменьшается.
м/мин, знак „-” означает, что паром приближается к берегу, т.е. x(t) уменьшается.
Ответ: V(t)= 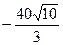 м/мин.
м/мин.
Задачи на экстремум.
 Задача. Заводу поручено изготовить резервуар емкостью 4м3 открытый сверху с квадратным основанием. При этом внутренняя поверхность должна быть покрыта оловом. Какими следует выбрать размеры резервуара, чтобы на его покрытие было израсходовано наименьшее количество олова?
Задача. Заводу поручено изготовить резервуар емкостью 4м3 открытый сверху с квадратным основанием. При этом внутренняя поверхность должна быть покрыта оловом. Какими следует выбрать размеры резервуара, чтобы на его покрытие было израсходовано наименьшее количество олова?
Алгоритм решения.
| 1. Выявить величину, о наибольшем или наименьшем значении которой говорится в задаче. | 1. Sпов. – наименьшая Sпов.=Sосн+Sбок=АВ2+4АВ·АА1 |
2.  Ввести переменную, задание которой определяет величину, указанную в задаче. Ввести переменную, задание которой определяет величину, указанную в задаче. | 2. Пусть АВ=х. Тогда V=x2·AA1, 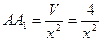 |
| 3. Указать допустимые значения для переменной. | 3. х>0 |
| 4. Выразить величину из пункта 1 как функцию переменной х. | 4. S(x)=x2+4∙x∙ 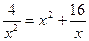 |
 5. Найти наибольшее или наименьшее значение функции (п.4) на интервале, указанном в п.3. 5. Найти наибольшее или наименьшее значение функции (п.4) на интервале, указанном в п.3. | 5. S’(x)=2x- 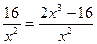 S’(x)=0; 2x3-16=0 x=2 S’(x) - + 0 S(x) 2 x т. min S’(x)=0; 2x3-16=0 x=2 S’(x) - + 0 S(x) 2 x т. min |
На интервале (0; +∞) функция S(x) определена и непрерывна и имеет единственную стационарную точку х=2 – т.min. Значит, minS(x)=S(2)
 (0; +∞)
(0; +∞)
Следовательно, чтобы на покрытие резервуара ушло наименьшее количество олова, его размеры должны быть равны AB=AD=2 (м), АА1= 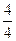 =1 (м).
=1 (м).
Ответ: 2х2х1.
Задача 1. Составляется электрическая цепь из двух параллельно соединенных сопротивлений. При каком соотношении между этими сопротивлениями, сопротивление всей цепи максимально, если при последовательном соединении этих сопротивлений оно равно 16 Ом?
Решение:
1. Обозначим r – сопротивление электрической цепи, состоящей из двух параллельно соединенных сопротивлений r1и r2. Тогда:
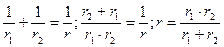
2. Пусть r1=x, тогда r2=16-x (т.к. r1+r2=R при последовательном соединении).
3. 0<x<16
4. Рассмотрим функцию:
r(x)= 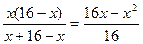 и найдем наибольшее значение этой функции на интервале (0; 16).
и найдем наибольшее значение этой функции на интервале (0; 16).
5. r΄(x)= 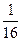 (16-2x); r΄(x)=0; 16-2x=0
(16-2x); r΄(x)=0; 16-2x=0
x=8
 r’(x)
r’(x)
0 + - x
r(x) 8 16
т.max
На интервале (0; 16) функция r(x) и определена и непрерывна и имеет единственную стационарную точку x=8 – т.max. Значит maxr(x)=r(8)
(0; 6)
r1=8; r2=16-8=8
Ответ: сопротивление всей цепи максимально, если r1=r2=8 Ом.
Задача 2. В питательную среду вносят популяцию из 1000 бактерий. Численность популяции возрастает по закону Р(t)=1000+ 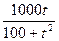 , где t – выражаетчся в часах.
, где t – выражаетчся в часах.
Найти максимальный размер этой популяции.
Решение: найдем наибольшее значение функции р(t) на интервале (0; +∞).
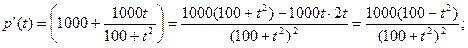
p’(t)=0; 100-t2=0; t=±10
p’(t)
 0 + - t
0 + - t
p(t) 10
т.max
На интервале (0; +∞) функция р(t) определена и непрерывна, и имеет единственную стационарную точку t=10 – т.max.
Значит maxp(x)=p(10)=1000+ 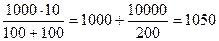
(0; +∞)
Ответ: максимальный размер популяции составляет 1050 особей и достигается по прошествии 10 часов роста.
Задача 3. Газовая смесь состоит из окиси азота (NO) и кислорода (О2). Найти концентрацию О2, при которой содержащаяся в смеси окись азота окисляется с наибольшей скоростью.
Решение: в условиях практической необратимости скорость реакции 2NO+O2=2NO2 выражается формулой V=kx2∙y, где x - концентрация NO, у – концентрация О2, а k – константа, зависящая от температуры. Концентрацию будем выражать в объемных процентах.
Пусть х – концентрация NО в любой момент времени.
Тогда 100-х – концентрация О2.
Рассмотрим функцию V(x)=k∙x2(100-x)=k(100x2-x3), где 0<x<100.
V’(x)=k(200x-3x2)=kx(200-3x)
V’(x)=0, x(200-3x)=0, x=0, x= 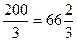
 V’(x)
V’(x)
0 + - x
V(x) 66 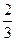 100
100
т.max
На интервале (0; 100) функция V(x) определена и непрерывна, и имеет единственную стационарную точку х=66 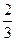 - т.max. Значит maxV(x)=V
- т.max. Значит maxV(x)=V 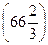 .
.
(0; 100)
Следовательно, скорость реакции наибольшая, если х=66 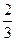 %; у=33
%; у=33 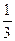 %.
%.
Ответ: концентрация О2 в смеси, при которой окись азота окисляется с наибольшей скоростью, составляет 33 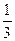 %.
%.
Задача 4. Два тела начинают двигаться одновременно по прямым Ох и Оу, пересекающимся под прямым углом. Первое тело движется со скоростью 10 м/с по прямой Ох от точки А к точке О, причем АО=100 м; второе тело движется со скоростью 5 м/с по прямой Оу от точки В к точке О причем ВО=200 м. Найдите наименьшее расстояние между телами во время движения.
Решение:
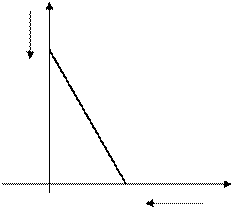 у В М V=5 м/с 200 м α 0 100 м К А V=10 м/с у В М V=5 м/с 200 м α 0 100 м К А V=10 м/с | Пусть t – время движения, по прошествии которого расстояние между телами будет наименьшим. Тогда 1-е тело будет находиться в точке К и ОК=100-10t, а 2-е – в точке М и ОМ=200-5t. По теореме Пифагора МК= 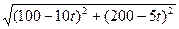 = = = = 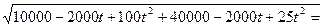 = = 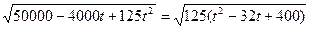 |
Рассмотрим функцию d(t)= 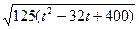 , и найдем ее наименьшее значение при t>0.
, и найдем ее наименьшее значение при t>0.
Так как функция d(t)>0 на интервале (0; +∞), то наименьшее значение функций d(t) и d2(t) достигается в одной и той же точке.
Поэтому, рассмотрим функцию d2(t)=125(t2-32t+400);
(d2(t))’=125(2t-32); (d2(t))’=0; 2t-32=0; t=16
(d2(t))’
 0 - + t
0 - + t
d(t) 16
т.min
На интервале (0; +∞) функция d(t) определена и непрерывна и имеет единственную стационарную точку t=16 – т.min.
Значит, mind(t)=d(16)= 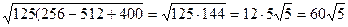 .
.
(0; +∞)
Таким образом, наименьшее расстояние между телами достигается по прошествии 16 с после начала движения и равно 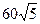 м.
м.
Ответ: 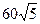 м.
м.
Задача 5. Стоимость бриллианта пропорциональна квадрату его массы. При обработке бриллиант массой 25 карат был расколот на две части. Каковы массы частей, если известно, что при этом произошла максимальная потеря стоимости?
Решение: стоимость бриллианта р=k∙m2, т.е.p=625k.
Пусть х – масса одного куска бриллианта, образовавшегося при расколе.
Тогда (25-х) – масса другой части.
kx2 – стоимость одной части, а k(25-x)2 – стоимость другой части, где 0<x<25.
f=625k-kx2-k(25-x)2 – потеря стоимости бриллианта в результате раскола (k – коэффициент пропорциональности).
Рассмотрим функцию:
f(x)=625k-kx2-k(25-x)2 и найдем ее наибольшее значение на интервале (0; 25).
f’(x)=-2kx+2k(25-x)=-4kx+50k
f’(x)=0; -4kx+50k=0;
-4x=-50; x= 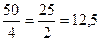
 f’(x)
f’(x)
0 + - x
 f(x) 12,5 25
f(x) 12,5 25
т.max
На интервале (0; 25) функция f(x) определена и непрерывна, и имеет единственную стационарную точку х=12,5 - т.max. Значит, maxf(x)=f(12,5).
(0; 25)
Следовательно, масса частей 12,5 карат и 12,5 карат.
Ответ: m1=m2=12,5 карат.
Литература:
 2020-04-12
2020-04-12 792
792







