Пример. Найти корни уравнения 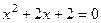 .
.
Решение. 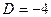 ,
, 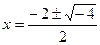 =
=  =
= 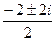 =
= 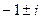 .
.
Ответ. 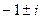 .
.
Кстати, как видно, получаются именно 2 взаимно сопряжённых корня.
Проверка. Подставим, например, 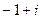 в уравнение.
в уравнение.
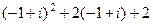 =
= 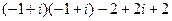 =
= 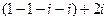 =
= 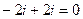 .
.
Действительную и мнимую часть 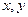 для числа
для числа 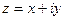 можно выразить через
можно выразить через 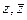 .
.
Докажем такие формулы: 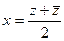 ,
, 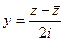
Доказательство.
Сложим 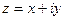 и
и 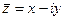 .
.
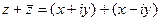 =
= 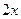 , тогда
, тогда 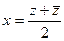 .
.
Вычтем 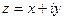 и
и 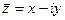 .
.
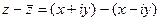 =
= 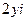 , тогда
, тогда 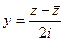 .
.
Тригонометрическая форма комплексного числа. Введём величину 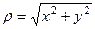 тогда
тогда 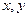 можно представить в таком виде:
можно представить в таком виде: 
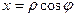 ,
, 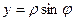 для некоторого
для некоторого 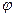 , ведь геометрически в этом случае
, ведь геометрически в этом случае 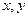 - катеты прямоугольного треугольника,
- катеты прямоугольного треугольника, 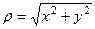 - его гипотенуза.
- его гипотенуза.
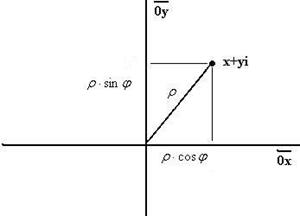
Абсцисса и ордината точки 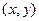 на плоскости это проекции на оси, они равны
на плоскости это проекции на оси, они равны 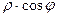 и
и 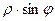 соответственно. Эти величины
соответственно. Эти величины 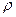 и
и 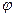 и есть полярные координаты точки на плоскости. Если записать комплексное число
и есть полярные координаты точки на плоскости. Если записать комплексное число  с помощью введённых выше величин
с помощью введённых выше величин 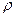 и
и 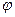 , получим:
, получим: 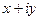 =
= 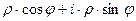 =
= 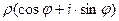 .
.
Выражение 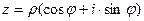 называется тригонометрической формой комплексного числа,
называется тригонометрической формой комплексного числа, 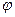 - его аргументом,
- его аргументом, 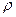 - модулем.
- модулем.
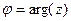
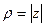 .
.
Понятие модуля согласуется с известным понятием, применявшимся раньше для отрицательных чисел: модуль - расстояние по кратчайшей линии до начала координат.
Для любой точки  модуль вычисляется как
модуль вычисляется как 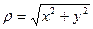 . Для вычисления аргумента верна формула
. Для вычисления аргумента верна формула 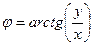 если точка в 4-й и 1-й четверти, либо
если точка в 4-й и 1-й четверти, либо 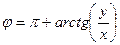 , если во 2-й и 3-й четверти.
, если во 2-й и 3-й четверти.
Так, число 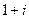 запишется в виде
запишется в виде 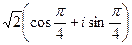 .
.
Число 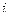 соответствует
соответствует 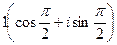 .
.
Если вычислить синус и косинус, то снова перейдём к обычной, «алгебраической» форме числа:
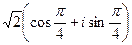 =
=  =
= 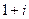 .
.
Действительное число имеет аргумент 0 (если оно положительно) или 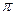 (если оно отрицательно).
(если оно отрицательно).
Угол может определяться разными способами, так, например, вместо угла 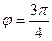 во всех вычислениях для комплексных чисел в тригонометрической форме можно использовать
во всех вычислениях для комплексных чисел в тригонометрической форме можно использовать  , и это не будет ошибкой, так как тригонометрические функции повторяются через промежуток
, и это не будет ошибкой, так как тригонометрические функции повторяются через промежуток  .
.
Умножение и деление в тригонометрической форме
В тригонометрической форме: 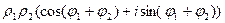
Докажем эту формулу.
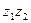 =
= 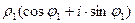
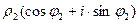 =
=
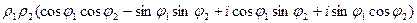 =
=
используем известные тригонометрические формулы косинуса суммы и синуса суммы, и получим 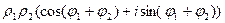 .
.
 2020-04-07
2020-04-07 230
230








