Формула деления двух комплексных чисел в тригонометрической форме:  =
= 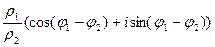 .
.
Для её доказательства достаточно домножить на 
 :
:
 =
=  =
=  =
=
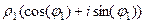 .
.
Для деления двух комплексных чисел, представленных в тригонометрической форме, нужно поделить их модули и вычесть аргументы.
Заметим, что при умножении на мнимую единицу  , а именно при действии
, а именно при действии  , фактически вектор
, фактически вектор  на плоскости переходит в
на плоскости переходит в 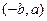 , то есть как раз и прибавляется аргумент числа
, то есть как раз и прибавляется аргумент числа 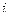 , то есть 90 0.
, то есть 90 0.
Примеры.
Умножить  . Во-первых, это можно сделать и без триг.формы:
. Во-первых, это можно сделать и без триг.формы:
 =
=  =
=  .
.
В тригонометрической форме: (используем представление чисел, которое сделали ранее).
 =
=  .
.  =
= 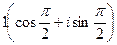 .
.
 =
= 
 =
=
 =
=  =
=
 =
= 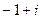 .
.
Поделить  .
.
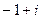 =
= 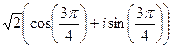 ,
,  =
=  . Тогда
. Тогда
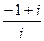 =
=  =
=
 =
=  =
=  .
.
Формула Эйлера
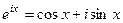
|
Доказательство.
Способ 1. 


Производная по  :
:
 =
=  =
=  .
.
Способ 2. Вспомним разложение экспоненты по формуле Тейлора. 
Тогда вычислим 
Но ведь  ,
,  ,
,  ,...
,...
Тогда  теперь соберём в отдельные слагаемые все части, где нет
теперь соберём в отдельные слагаемые все части, где нет  , и где есть
, и где есть 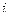 .
.
 но ведь в 1 и 2 скобках - разложения
но ведь в 1 и 2 скобках - разложения  и
и  . Итак,
. Итак,  , что и требовалось доказать.
, что и требовалось доказать.
 =
=  ,
,
 =
=  =...
=...
Воспользуемся чётностью cos и нечётностью sin. Тогда:
 =
=  .
.
Для любого числа  можно вычислить
можно вычислить  :
:
 =
= 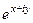 =
=  =
=  =
=  .
.
Для сопряжённого числа можно вычислить аналогично:
 =
= 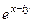 =
= 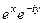 =
=  =
=  .
.
То есть, сопряжённое под знаком экспоненты приводит к сопряжённому результату.
Показательная форма комплексного числа.
По формуле Эйлера, выражение 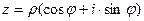 может быть записано в виде
может быть записано в виде  .
.
Так, например, мнимой единице соответствует аргумент  и модуль 1, поэтому запись в тригонометрической и показательной формах такова:
и модуль 1, поэтому запись в тригонометрической и показательной формах такова:
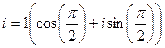
 .
.
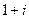 =
= 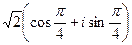

Умножение и деление в тригонометрической и показательной форме.
Умножение, и особенно деление комплексных чисел чаще всего бывает легче выполнять в тригонометрической форме, чем в алгебраической, так как для деления не нужно домножать на сопряжённое в знаменателе.
В показательной форме.
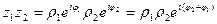

Пример. Поделить  .
.
Решение.  =
=  =
= 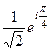 =
=  =
=
 =
=  .
.
ЛЕКЦИЯ № 7. 03.03.2020
 2020-04-07
2020-04-07 195
195








