Области в комплексной плоскости и неравенства, задающие их

 правая полуплоскость.

 верхняя полуплоскость.

 - окружность радиуса R вокруг начала координат. 

 - круг радиуса R вокруг начала координат. 

 это круг радиуса 1 вокруг точки . Это неравенство задаёт следующее условние: удаление числа 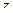 от фиксированного числа  не превышает 1. Можно непосредственно преобразовать в уравнение круга в плоскости:  а это уравнение круга, центр которого в точке (0,1), то есть как раз в точке . Чертёж:

 

Пример.  это круг радиуса 2 с центром в точке , то есть точке (1,1) в плоскости.

Пример. Множество  это кольцо вокруг точки .

Пример.  это круг радиуса  вокруг точки .

Функции комплексного переменного.

Обобщим на комплексную плоскость синус и косинус.

Верны такие формулы: , .

Доказательство.

Рассмотрим для действительного числа  и покажем, что данные функции, а именно  и , приведут именно к обычному синусу и косинусу действительного числа, т.е. они обобщают синус и косинус. Используя формулу Эйлера,

1)  =  =  =

2)  =  =  =

 

Неограниченность синуса и косинуса в комплексной плоскости.

Пример. .

Вычислим:  =  = .

 

Логарифм комплексного числа.

 

Обобщённый логарифм вводится с помощью формулы:  

.

Доказательство.

 

,

это означает  так как синус и косинус не зависят от прибавления угла, кратного  . Это равенство уже очевидно, так как это и есть тригонометрическая форма комплексного числа.  

Если вычислять логарифм положительного действительного числа, то , т.е. одна точка из бесконечного множества попадает на действительную ось, потому что исходный угол . Для любого числа, которое не является действительным положительным, , поэтому происходит сдвиг этой последовательности на часть деления, и ни одна точка не попадёт на действительную ось.

Пример. Вычислить .

Здесь , . Поэтому  = .

Точки в комплексной плоскости: , , , и так далее.

Ни одного значения на действительной оси нет, и здесь, по сравнению со значениями логарифма положительного числа, сдвиг на половину деления: одна точка ушла вверх с действительной оси, а другая ещё не достигла этой оси. Чертёж:

Пример. Вычислить .

 = . Последовательность значений такова:  каждая соседняя пара отличается на  по высоте. Здесь сдвиг вверх всего на четверть деления, а не на половину, как для .

1) При фиксированном модуле исходного числа и увеличении его аргумента, эта последовательность точек плывёт вверх, при полном повороте на  как раз следующая точка попадёт на место предыдущей.

2) При фиксированном аргументе исходного числа и увеличении его модуля, эта последовательность точек плывёт вправо, если исходная точка внутри единичной окружности то множество значений логарифма в левой полуплоскости, так как , а если вне единичной окружности, то в правой полуплоскости.

Динамическая анимация, показывающая поведение значений  в зависимости от колебаний модуля или аргумента , показана в следующем обучающем видеоролике: 

http://www.youtube.com/watch?v=LKFFn-TSLd0 

 

Замечание. Единственная точка в комплексной плоскости, для которой не существует логарифма, это 0. Ведь в этом случае , и не существует .

 

Пример. Вычислить .

Решение. Представим , расположенную в основании, в виде . Тогда , причём чуть выше мы вычисляли

. Тогда  =  =  т.е. получается бесконечное множество точек на действительной оси.

 

       Для всякой функции  можно отдельно выделить действительную и мнимую части, и представить в виде

. Таким образом, возникают понятия: действительная и мнимая часть функции, обозначения: , . Итак, комплексной функции можно поставить в соответствие некоторое отображение из  в , а именно . Но график такого отображения был бы в 4-мерном пространстве, поэтому изобразить его в нашем 3-мерном пространстве невозможно. Но мы можем пользоваться неким подобием графика, а именно, рассматривать чертёж искажений плоскости, изучать, в какие линии отображаются горизонтальные либо вертикальные линии из исходной плоскости.

 

Пример.  Разложить  на сумму действительной и мнимой частей, изобразить искажения плоскости при переходе .

1)  =  =  = .

Таким образом, , .

Чтобы исследовать, куда переходят горизонтальные прямые, зафиксируем , при этом  изменяется от  до , пусть движение задано с помощью параметра :

.

Чтобы составить уравнение, взаимосвязывающее , и узнать, какая это кривая, исключим параметр , выразив из второго уравнения: , тогда . Это парабола, лежащая на боку, ветвями направленная вправо, причём чем больше , тем левее вершина, и тем более пологая парабола получается, ведь  при этом меньше. А если , то возникает предельный случай: обе ветви смыкаются в одну линию и образуют правую полуось. Действительная ось отображается на правую полуось в плоскости .

Аналогично, для какой-либо вертикальной прямой:

. Тогда, исключая параметр , получим . Это параболы, направленные ветвями влево, симметричные тем, что были рассмотрены чуть выше.

На чертеже зелёным цветом показаны горизонтальные прямые и их образы при отображении , а красным - вертикальные прямые и их образы:

Пример.  Разложить  на сумму действительной и мнимой частей.

Используем то, что нашли ранее: , тогда

 = = .

Здесь .

ЛЕКЦИЯ № 8. 10.03.2020

Пример.  Разложить  на действительную и мнимую часть.

По формуле Эйлера:  =  =  =  = , тогда , . 

 

 

       Изучим подробнее линейное отображение, какие деформации плоскости происходят при действии линейной функции вида , где коэффициенты ,  это тоже некоторые комплексные числа. При этом очевидно, что  приводит к сдвигу плоскости на вектор , поэтому сначала более подробно изучим именно  без сдвига.

 = . Но такое отображение можно представить с помощью линейного оператора:

 = .

Введём величину , тогда существует какой-то угол  , для которого , . Причём заметим, что это именно ,  для исходного комплексного числа.

Тогда матрица линейного оператора имеет вид:  то есть это композиция растяжения и поворота плоскости, причём поворот на угол , а растяжение или сжатие на .

Доказали, что линейное отображение  в комплексной плоскости есть композиция растяжения, поворота и сдвига.

       На этом чертеже показано, как изменяется плоскость при линейном отображении. Красным веделено горизонтальное направление, после отображения оно повёрнуто.

           

 Замечание. Отображение  соответствует зеркальному отражению плоскости, т.е. оно не сводится к композиции поворота и растяжения.