2020-04-07
194
Возводить комплексные числа в степень можно с помощью такой формулы: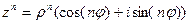 
она называется формулой Муавра и позволяет не перемножать множество скобок, если требуется вычислить большую степень числа
Доказательство. Если умножим в тригонометрической форме не два разных числа, а одно и то же число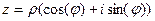 
, то получим:
= 
.
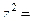
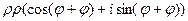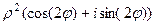Таким же образом можно умножить 
в третий раз и снова в аргументе прибавится 
, а модуль снова умножится на 
.
=
= 
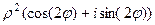
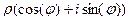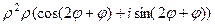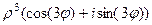
Таким образом, по индукции, можно доказать, что
= 
.
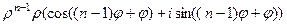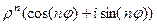Но ещё легче возводить в степень с помощью показательной формы числа: 
, здесь даже доказывать по индукции нет необходимости.
Пример. Найти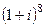 
по формуле Муавра.
Вычислим модуль и аргумент.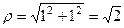 
.
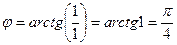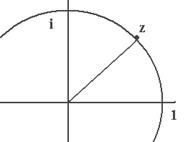
Таким образом, соответствующая точка расположена в первой четверти на пересечении биссектрисы угла и единичной окружности.
По формуле Муавра,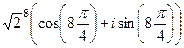 
= 
= 
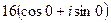= 16.
В показательной форме: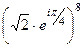 
= 
= 
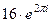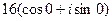= 16.
Корень порядка n вычисляется по такой формуле:
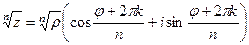
Доказательство. Если возведём в степень n, получим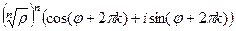 
= 
.
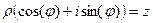Добавка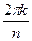 
после возведения в степень станет кратной 
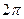, то есть точка, отстоящие на угол 
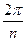, просто опишет один лишний оборот вокруг начала координат, то есть в аргументу добавится 360 градусов, и придёт в ту же точку, что и без 
.
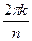Пример. Найдите все значения корня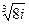 
.
Сначала представим комплексное число, которое находится под знаком корня, в тригонометрической форме.
Точка расположена на мнимой оси выше начала координат, поэтому аргумент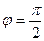 
, модуль 
.
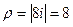Теперь находим все 3 корня.
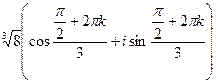при k = 0,1,2. 
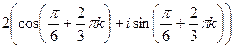, отсюда:
1) 
= 
= 
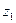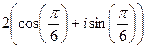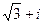
2) 
= 
= 
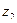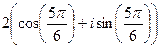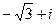
3) 
= 
= 
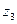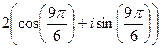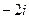
Чертёж:
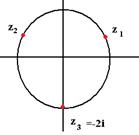
Если к исходному углу добавить 120 градусов, то для куба этого числа добавится 360 градусов, и результат будет точно такой же. С этим фактом как раз и связано наличие лишнего слагаемого 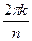в формуле.
Квадратных корней два, а именно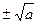 
. Это происходит по той же причине: если число было положительным, то его аргумент был 0, и тогда по формуле 
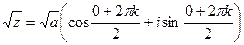то есть
= 
= 
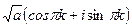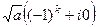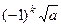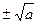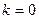, что и соответствует при 
и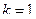 
. К аргументу прибавляется по 360 / 2 = 180 градусов.
