Пусть  – группа,
– группа, 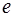 – ее единичный элемент,
– ее единичный элемент,  .
.
Определение. Порядком элемента  группы называется наименьшее натуральное число
группы называется наименьшее натуральное число  , такое, что
, такое, что  . Если
. Если  для любого натурального числа
для любого натурального числа  , то
, то  называют элементом бесконечного порядка.
называют элементом бесконечного порядка.
Примеры
5.1. В мультипликативной группе комплексных чисел 
1) порядок 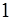 равен
равен 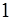 , так как
, так как  ;
;
2) порядок  равен
равен  , так как
, так как  ,
,  ;
;
3) порядок  равен 3, так как
равен 3, так как  ,
,  ,
,  ;
;
4) порядок  равен
равен  , так как
, так как  ,
,  ,
,  ,
,  ;
;
5) порядок  равен
равен  , так как
, так как  ,
,  ,
,  ,
, 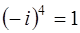 ;
;
6) число  – элемент бесконечного порядка, так как
– элемент бесконечного порядка, так как  при
при  .
.
5.2. В мультипликативной группе невырожденных квадратных матриц второго порядка с действительными элементами
1) порядок матрицы  равен
равен  , так как
, так как  ,
,  =
= 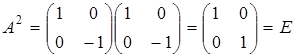 ;
;
2) порядок матрицы  равен
равен  , так как
, так как  ,
,  ,
,  ,
,
 ;
;
3) матрица  – элемент бесконечного порядка, так как
– элемент бесконечного порядка, так как  ,
,
 ,
,  , можно доказать методом математической индукции
, можно доказать методом математической индукции 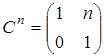 при
при  .
.
Циклические группы
Определение. Мультипликативная группа  называется циклической, если основное множество группы состоит из степеней какого-либо одного элемента группы; этот элемент называется образующим элементом группы.
называется циклической, если основное множество группы состоит из степеней какого-либо одного элемента группы; этот элемент называется образующим элементом группы.
 , где
, где 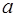 – образующий элемент.
– образующий элемент.
Определение. Аддитивная группа  называется циклической, если ее основное множество состоит из кратных какого-либо одного элемента группы; этот элемент называется образующим элементом группы.
называется циклической, если ее основное множество состоит из кратных какого-либо одного элемента группы; этот элемент называется образующим элементом группы.
 , где
, где 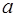 – образующий элемент группы.
– образующий элемент группы.
Теорема 1. Все бесконечные циклические группы изоморфны между собой. Все конечные циклические группы порядка  изоморфны между собой.
изоморфны между собой.
Теорема 2. Любая подгруппа циклической группы есть циклическая группа.
Примеры
5.4.  – аддитивная группа целых чисел.
– аддитивная группа целых чисел.
 или
или

следовательно,  – циклическая группа с образующим элементом
– циклическая группа с образующим элементом  или
или  .
.
5.5. Аддитивная группа  является циклической с образующим элементом
является циклической с образующим элементом  или
или 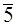 . Этот результат следует из примера 5.3.
. Этот результат следует из примера 5.3.
5.6. Выясните, является ли мультипликативная группа корней 6-ой степени из 1 циклической. Если да, то найдите все ее образующие элементы.
Решение.
 , где
, где 
 – единичный элемент. Найдем порядок каждого элемента группы, для чего используем таблицу Кэли задачи 1.10.
– единичный элемент. Найдем порядок каждого элемента группы, для чего используем таблицу Кэли задачи 1.10.
 , порядок
, порядок  равен
равен  ;
;
 ,
,  ,
,  ,
,  ,
,  ,
,  , порядок
, порядок 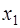 равен 6, видим, что множество
равен 6, видим, что множество  состоит из степеней элемента
состоит из степеней элемента  , следовательно, группа
, следовательно, группа  – циклическая, с образующим элементом
– циклическая, с образующим элементом  ;
;
 ,
,  ,
,  , порядок
, порядок  равен
равен  ;
;
 ,
,  , порядок
, порядок  равен
равен  ;
;
 ,
,  ,
,  , порядок
, порядок  равен
равен  ;
;
 ,
, 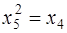 ,
,  ,
, 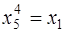 ,
,  ,
,  , порядок
, порядок  равен
равен  . Видим, что элемент
. Видим, что элемент  также является образующим элементом данной группы.
также является образующим элементом данной группы.
Вывод: группа  является циклической, с образующим элементом
является циклической, с образующим элементом 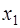 или
или  .
.
5.7. Найдите порядок каждого элемента симметрической группы 3-ей степени. Выясните, какие циклические подгруппы данной группы они порождают.
Решение.
Дана группа  , где
, где  ,
,  – единичный элемент данной группы.
– единичный элемент данной группы.
При решении используем результаты примера 2.7:
 , порядок
, порядок  равен
равен  . Единичная подгруппа
. Единичная подгруппа  – циклическая;
– циклическая;
 ,
,  , порядок
, порядок  равен
равен  . Кроме того, подгруппа
. Кроме того, подгруппа  является циклической, с образующим элементом
является циклической, с образующим элементом  ;
;
 ,
,  ,
,  , порядок
, порядок  равен
равен  , а подгруппа
, а подгруппа  является циклической, с образующим элементом
является циклической, с образующим элементом  ;
;
Аналогично:
 ,
, 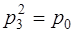 , порядок
, порядок  равен
равен  , подгруппа
, подгруппа  – циклическая, с образующим элементом
– циклическая, с образующим элементом  ;
;
 ,
,  ,
,  , порядок
, порядок  равен
равен  . Видим, что элемент
. Видим, что элемент  еще один образующий элемент подгруппы
еще один образующий элемент подгруппы 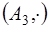 ;
;
 ,
,  , порядок
, порядок 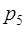 равен
равен  , подгруппа
, подгруппа  – циклическая, с образующим элементом
– циклическая, с образующим элементом 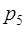 .
.
Вывод: группа  циклической не является, но все подгруппы этой группы, кроме самой группы, циклические. Подгруппа
циклической не является, но все подгруппы этой группы, кроме самой группы, циклические. Подгруппа 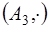 имеет два образующих элемента
имеет два образующих элемента  и
и  .
.
5.8. Докажите, что множество  , состоящее из матриц
, состоящее из матриц  ,
,  ,
,  ,
, 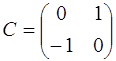 , является подгруппой мультипликативной группы невырожденных квадратных матриц 2-го порядка с действительными элементами. Является ли эта группа абелевой? Является ли она циклической? Каковы ее образующие элементы?
, является подгруппой мультипликативной группы невырожденных квадратных матриц 2-го порядка с действительными элементами. Является ли эта группа абелевой? Является ли она циклической? Каковы ее образующие элементы?
Решение:
 .
.
Составим таблицу умножения для матриц из множества 
| × | 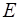 |  |  |  |
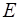 | 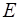 |  |  |  |
 |  | 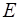 |  |  |
 |  |  |  | 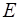 |
 |  |  | 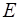 |  |
Из таблицы видим, что умножение – алгебраическая операция в  , операция умножение – коммутативна, так как таблица симметрична относительно главной диагонали, в алгебре
, операция умножение – коммутативна, так как таблица симметрична относительно главной диагонали, в алгебре 
 ,
,  ,
,  ,
,  . По критерию подгруппы, алгебра
. По критерию подгруппы, алгебра  - подгруппа мультипликативной группы невырожденных матриц с действительными элементами, причем абелева.
- подгруппа мультипликативной группы невырожденных матриц с действительными элементами, причем абелева.
Найдем порядок каждого элемента подгруппы 
 , следовательно, порядок
, следовательно, порядок 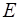 равен
равен  ;
;
 ,
,  , порядок
, порядок  равен
равен  ;
;
 ,
,  ,
,  ,
,  , порядок
, порядок  равен
равен  , кроме того подгруппа
, кроме того подгруппа  – циклическая, так как множество G состоит из степеней матрицы
– циклическая, так как множество G состоит из степеней матрицы  , т.е. матрица
, т.е. матрица  является образующим элементом подгруппы
является образующим элементом подгруппы  ;
;
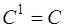 ,
,  ,
,  ,
,  , порядок
, порядок  равен 4, матрица
равен 4, матрица  – образующий элемент подгруппы
– образующий элемент подгруппы  .
.
Изоморфизм групп
Пусть даны группы  и
и  .
.
Определение. Группы  и
и  называются изоморфными, если существует отображение j множества
называются изоморфными, если существует отображение j множества  на множество
на множество  , удовлетворяющее условиям:
, удовлетворяющее условиям:
1)  - инъективное отображение множества
- инъективное отображение множества  на множество
на множество  , т.е.
, т.е.
 если
если  , то
, то  ;
;
2)  ,
,  .
.
Обозначают  .
.
Примеры
6.1. Докажем, что аддитивная группа целых чисел изоморфна аддитивной группе четных чисел.
Решение.
 и
и  – данные группы.
– данные группы.  .
.
Зададим отображение  множества
множества  на множество
на множество  формулой:
формулой: 
 ,
,  :
:
1)  - инъективное отображение, так как для любых
- инъективное отображение, так как для любых  и
и 
 ,
,  и если
и если 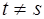 , то
, то  , т.е.
, т.е.  ;
;
2) 
 .
.
По определению,  - изоморфизм группы
- изоморфизм группы  на группу
на группу  , следовательно,
, следовательно,  .
.
6.2. Докажите, что аддитивная группа четных чисел изоморфна мультипликативной группе целых степеней числа  .
.
Решение:
Даны группы  ,
,  , где
, где  ,
, 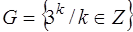 .
.
Зададим отображение  множества
множества  на множество
на множество  формулой
формулой 
 ,
,  :
:
1) отображение  - инъективное, так как
- инъективное, так как  ,
,  ,
,  и если
и если  , то
, то 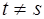 ,
, 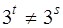 , и
, и  ;
;
2) 
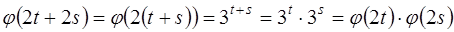 .
.
По определению,  .
.
6.3. Докажите, что аддитивная группа действительных чисел изоморфна мультипликативной группе положительных действительных чисел.
Решение:
 и
и  – данные группы.
– данные группы.
Зададим отображение  множества
множества  на множество
на множество  формулой
формулой 
 ,
,  :
:
1. отображение  - инъективное, так как
- инъективное, так как 
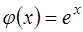 ,
,  и если
и если  , то
, то  , то есть
, то есть  ;
;
2. 
 .
.
По определению, 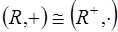 .
.
6.4. Докажите, что мультипликативная группа матриц вида  ,
,  изоморфна аддитивной группе действительных чисел.
изоморфна аддитивной группе действительных чисел.
Решение:
Пусть  , где
, где  ,
,  – данные группы.
– данные группы.
Зададим отображение  множества
множества  на множество
на множество  формулой:
формулой:
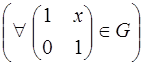
 ,
, 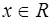 :
:
1.  - инъективное отображение, так как
- инъективное отображение, так как 
 ,
,  , если
, если  , то
, то  ;
;
2. 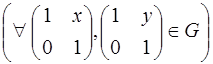 ,
, 
 .
.
По определению,  - изоморфизм группы
- изоморфизм группы  на группу
на группу  , следовательно,
, следовательно,  .
.
 2020-04-12
2020-04-12 8639
8639
