Операции над идеалами

Пусть 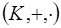 - произвольное кольцо,  I и J -   идеалы этого кольца.

Определение. Суммой идеалов I и J кольца 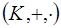 называется множество

I + J, определяемое равенством I + J= .

Определение. Произведением идеалов I и J кольца 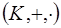 называется множество I J, определяемое равенством IJ= .

Определение.  Пересечением идеалов I и J кольца  называется множество .

 Легко доказать, что сумма, произведение, пересечение идеалов кольца есть идеал этого кольца.

Примеры.

4.5. Найдите идеал (2): а) в ; б) в  в) в ; г) в .

Решение: По определению главного идеала кольца 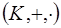, порожденного элементом 2,  

а) в кольце   

,  есть множество четных чисел.

б) в кольце

 есть множество целых гауссовых чисел с четными действительной частью и коэффициентом при мнимой части.

в) в кольце

.

 есть множество многочленов с четными коэффициентами.

г) в кольце   

.

 есть множество многочленов с рациональными коэффициентами.

4.6. В кольце    найдите идеал, порожденный элементами и 4.

Решение: По определению идеала, порожденного элементами данного кольца 

, где ,

.

4.7.  Какие из чисел  принадлежат идеалу (  кольца целых гауссовых чисел? Какие из них порождают этот идеал?

Решение: По определению главного идеала,

.

a) Выясним, можно ли число  представить в виде

,

.

б) аналогично, для числа  получаем

, значит,  и, следовательно, .

в) для числа  получаем

, значит,  и, следовательно, .

Выясним, какие из чисел  порождают идеал , т.е. можно ли любой элемент  представить в виде     или в виде   

Для имеем

 где    может не принадлежать . Следовательно, число не порождает идеал .

, где  .

Следовательно, элемент порождает идеал