2020-04-12
944
Пусть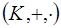 
- произвольное кольцо.
Определение. Отличный от нуля элемент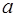 
кольца 
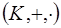называется делителем нуля в данном кольце, если в 
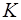существует отличный от нуля элемент 
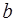, такой, что 
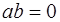или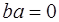 
(разумеется, в этом случае и элемент 
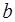является делителем нуля в ).
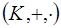Определение. Областью целостности называется коммутативное кольцо, содержащее не менее двух элементов, без делителей нуля.
Примеры
6.1. В кольце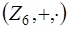 
классов вычетов по модулю 
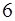делителями нуля являются классы 
, 
, 
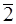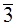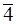, т.к. 
, 
.
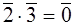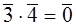6.2. В кольце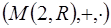 
квадратных матриц второго порядка с действительными элементами делителями нуля являются, например, матрицы
, 
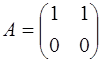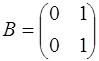, так как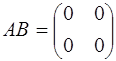 
, 
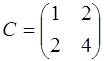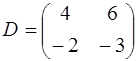, так как 
.
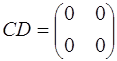6.3. В кольце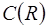 
функций, непрерывных на множестве 
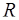, делителями нуля являются, например, функции
, 
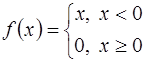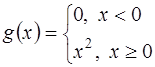, так как 
.
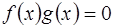Отсюда следует, что кольца из приведенных примеров областями целостности не являются.
6.4. Любое поле является областью целостности.
Действительно, пусть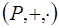 
- поле. Пусть элемент 
, 
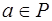является делителем 
. Тогда существует 
, 
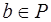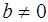такой, что 
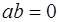(1).
По определению поля, для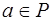 
, 
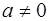существует элемент 
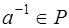, обратный 
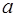, то есть 
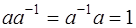. Умножим обе части равенства (1) на 
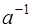. Получим 
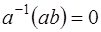, то есть 
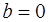. Полученное противоречие доказывает, что в поле 
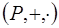нет делителей нуля, следовательно, 
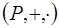- область целостности.
|
|
|
6.5.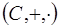 
- поле комплексных чисел, а значит, область целостности. В 
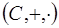нет делителей нуля, тогда их нет ни в одном числовом кольце. Следовательно, все числовые кольца, содержащие не менее двух элементов, являются областями целостности. В частности, 
, 
, 
, 
, 
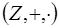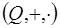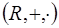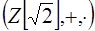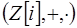и т.п.
Простейшие свойства делимости в коммутативном кольце
