6.6. Докажите, что следующие аддитивные группы изоморфны между собой:
а)  ,где
,где  и
и  , где
, где 
б)  и
и  ;
;
в)  и
и  ;
;
г)  , где
, где  и
и  ;
;
д)  , где
, где  и
и  , где
, где  .
.
6.7. Докажите, что мультипликативная группа невырожденных квадратных матриц вида  , где
, где 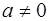 ,
,  изоморфна мультипликативной группе действительных чисел
изоморфна мультипликативной группе действительных чисел  .
.
6.8. Среди следующих групп укажите все пары изоморфных между собой групп:  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
6.9. Докажите, что мультипликативная группа матриц
 изоморфна мультипликативной группе корней 4-ой степени из 1.
изоморфна мультипликативной группе корней 4-ой степени из 1.
Кольца
Понятие кольца
Рассмотрим алгебру с двумя бинарными алгебраическими операциями. Операции будем называть сложением и умножением и обозначать  .
.
Определение. Алгебра 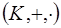 с двумя бинарными алгебраическими операциями называется кольцом, если:
с двумя бинарными алгебраическими операциями называется кольцом, если:
1) алгебра  есть абелева группа;
есть абелева группа;
2) операция умножения ассоциативна, то есть для любых  ,
,  ;
;
3) Операция умножения дистрибутивна относительно операции сложения, то есть для любых  ,
,  и
и  .
.
Если операция умножения коммутативна, то есть для любых  ,
,  , то кольцо называется коммутативным.
, то кольцо называется коммутативным.
Если кольцо 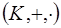 содержит элемент
содержит элемент  , нейтральный относительно умножения, то
, нейтральный относительно умножения, то  называется единицей кольца, кольцо
называется единицей кольца, кольцо 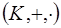 называется кольцом с единицей.
называется кольцом с единицей.
Примеры
1.1. Алгебра  – коммутативное кольцо с единицей. Действительно:
– коммутативное кольцо с единицей. Действительно:
1) алгебра  – абелева группа;
– абелева группа;
2) операция умножения ассоциативна в  ;
;
3) операция умножения в  дистрибутивна относительно сложения.
дистрибутивна относительно сложения.
Кроме того, выполняется коммутативный закон умножения.
Кольцо 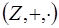 называется кольцом целых чисел.
называется кольцом целых чисел.
1.2. Аналогично, алгебры  ,
,  ,
,  – коммутативные кольца с единицей.
– коммутативные кольца с единицей.
1.3. Пусть  – множество целых чисел, кратных данному натуральному числу
– множество целых чисел, кратных данному натуральному числу  .
.
 .
.
В первой части доказано, что  – абелева группа.
– абелева группа.
Докажем, что умножение – алгебраическая операция в  , то есть
, то есть 
 .
.
Действительно:
 ,
,  , где
, где  , тогда
, тогда  , где
, где  , значит,
, значит,  и умножение – алгебраическая операция в
и умножение – алгебраическая операция в  .
.
Рассмотрим алгебру  :
:
1)  – абелева группа;
– абелева группа;
2) коммутативный, ассоциативный законы умножения, дистрибутивный закон умножения относительно сложения в  выполняется, так как они выполняются в
выполняется, так как они выполняются в  , а
, а  .
.
Алгебра  - коммутативное кольцо, которое называется кольцом целых чисел, кратных данному натуральному числу
- коммутативное кольцо, которое называется кольцом целых чисел, кратных данному натуральному числу  .
.
1.4. Рассмотрим множество  чисел вида
чисел вида  , где
, где 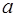 и
и 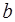 – целые числа.
– целые числа.
 .
.
Докажем, что сложение и умножение – алгебраические операции в  , то есть
, то есть 
 ,
,  .
.
Действительно:
 ,
,  ,
,  ;
;  ,
,  , значит,
, значит,  ,
,  ,
,  , значит
, значит  . Следовательно, сложение и умножение - алгебраические операции в
. Следовательно, сложение и умножение - алгебраические операции в  .
.
Рассмотрим алгебру  :
:
а) коммутативный, ассоциативный законы сложения и умножения, дистрибутивный закон умножения относительно сложения в  выполняются, так как они выполняются в
выполняются, так как они выполняются в  , а
, а  ;
;
б)  , так как
, так как  ,
,  ;
;
в) 
 .
.
Действительно:
 ,
, 
 ,
,  , значит,
, значит,  .
.
Вывод: Алгебра  – коммутативное кольцо с единицей.
– коммутативное кольцо с единицей.
1.5. Аналогично, алгебра  – коммутативное кольцо с единицей.
– коммутативное кольцо с единицей.
1.6. Рассмотрим множество чисел вида  ,
,  – мнимая единица,
– мнимая единица,  . Сложение и умножение – алгебраические операции в
. Сложение и умножение – алгебраические операции в  , так как для любых
, так как для любых 
 ,
,  .
.
Действительно:
 ,
,  ,
,  .
.
 .
.  , причем
, причем  ,
,  ,
,  ,
,  – целые числа, значит
– целые числа, значит  ,
,  .
.
Рассмотрим алгебру  :
:
а) коммутативный, ассоциативный законы сложения и умножения, дистрибутивный закон умножения относительно сложения в  выполняются, так как они выполняются в
выполняются, так как они выполняются в  , а
, а  ;
;
б)  , так как
, так как  , где
, где  ;
;
в) 
 .
.
Действительно,  ,
,  ,
,  , причем
, причем  , значит,
, значит,  .
.
Вывод. Алгебра  является коммутативным кольцом с единицей. Это кольцо впервые изучал великий немецкий математик Карл Фридрих Гаусс. Поэтому кольцо
является коммутативным кольцом с единицей. Это кольцо впервые изучал великий немецкий математик Карл Фридрих Гаусс. Поэтому кольцо  называют кольцом целых гауссовых чисел.
называют кольцом целых гауссовых чисел.
Элементами колец из примеров 1.1 – 1.6 являются числа с обычными операциями сложения и умножения. Такие кольца называются числовыми.
Рассмотрим несколько примеров колец, не являющихся числовыми:
1.7. Пусть  – произвольное числовое кольцо.
– произвольное числовое кольцо.
Из теории многочленов известно, что множество всех многочленов от переменной  с коэффициентами из
с коэффициентами из 
 образует коммутативное кольцо относительно сложения и умножения многочленов. В частности,
образует коммутативное кольцо относительно сложения и умножения многочленов. В частности,  – кольцо многочленов с целыми коэффициентами;
– кольцо многочленов с целыми коэффициентами;  ,
,  ,
,  – кольца многочленов соответственно с рациональными, действительными и комплексными коэффициентами.
– кольца многочленов соответственно с рациональными, действительными и комплексными коэффициентами.
1.8. Пусть  – произвольное числовое кольцо. Обозначим
– произвольное числовое кольцо. Обозначим  множество квадратных матриц порядка
множество квадратных матриц порядка  с элементами из
с элементами из  . Из теории матриц известно, что множество
. Из теории матриц известно, что множество  образует кольцо относительно сложения и умножения матриц. Это кольцо не коммутативное. Например
образует кольцо относительно сложения и умножения матриц. Это кольцо не коммутативное. Например  – кольцо квадратных матриц второго порядка с действительными элементами.
– кольцо квадратных матриц второго порядка с действительными элементами.
1.9. Рассмотрим множество всех действительных функций, непрерывных на множестве  . Это множество обозначим
. Это множество обозначим  . Сложение и умножение – алгебраические операции на множестве
. Сложение и умножение – алгебраические операции на множестве  , так как сумма и произведение функций, непрерывных на множестве
, так как сумма и произведение функций, непрерывных на множестве  , есть функции, непрерывные на множестве
, есть функции, непрерывные на множестве  . Непосредственная проверка показывает, что алгебра
. Непосредственная проверка показывает, что алгебра  – коммутативное кольцо с единицей.
– коммутативное кольцо с единицей.
Подкольца
Определение. Пусть 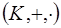 – кольцо,
– кольцо,  , сложение и умножение – алгебраические операции в
, сложение и умножение – алгебраические операции в  . Алгебра
. Алгебра  называется подкольцом кольца
называется подкольцом кольца  , если она сама является кольцом.
, если она сама является кольцом.
Примеры
2.1.  ,
,  ,
,  ,
,  – кольца, причем
– кольца, причем  , следовательно
, следовательно  ,
,  ,
,  ,
,  – подкольца кольца
– подкольца кольца  .
.
2.2.  ,
,  – кольца, причем
– кольца, причем  , следовательно,
, следовательно,  – подкольцо кольца
– подкольцо кольца  .
.
2.3.  – произвольное кольцо, по определению кольца,
– произвольное кольцо, по определению кольца,  .
.  – кольцо, причем
– кольцо, причем  и
и  , значит,
, значит,  и
и 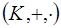 – подкольца кольца
– подкольца кольца 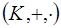 .
.
Критерий подкольца
Пусть 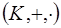 – кольцо,
– кольцо,  , сложение и умножение – алгебраические операции в
, сложение и умножение – алгебраические операции в  . Для того, чтобы алгебра
. Для того, чтобы алгебра  была подкольцом кольца
была подкольцом кольца  , необходимо и достаточно, чтобы
, необходимо и достаточно, чтобы 
 .
.
Примеры
2.4. Пусть  - кольцо квадратных матриц 2-го порядка с действительными элементами,
- кольцо квадратных матриц 2-го порядка с действительными элементами,  – множество всех диагональных квадратных матриц 2-го порядка, то есть множество матриц вида
– множество всех диагональных квадратных матриц 2-го порядка, то есть множество матриц вида  . Докажите, что множество L образует относительно сложения и умножения подкольцо кольца
. Докажите, что множество L образует относительно сложения и умножения подкольцо кольца  .
.
Решение:
 . Очевидно,
. Очевидно,  . Докажем, что сложение и умножение – алгебраические операции в
. Докажем, что сложение и умножение – алгебраические операции в  , то есть
, то есть  ,
,  ,
,  .
.
Действительно:
 ,
,  ,
,  .
.  ,
,  .
.  .
.  ,
,  ,
,  .
.
Рассмотрим алгебру  :
: 
 .
.
Действительно,  ,
,  , значит,
, значит,  . По критерию подкольца,
. По критерию подкольца,  подкольцо кольца
подкольцо кольца  .
.
Поля
Рассмотрим алгебру  с двумя бинарными алгебраическими операциями. Операции будем называть сложением и умножением и обозначать
с двумя бинарными алгебраическими операциями. Операции будем называть сложением и умножением и обозначать  .
.
Определение. Алгебра  , содержащая не менее двух элементов называется полем, если:
, содержащая не менее двух элементов называется полем, если:
4) алгебра  есть коммутативное кольцо;
есть коммутативное кольцо;
5) в Р существует единичный элемент, т.е.  ae=ea=a;
ae=ea=a;
6)  существует обратный элемент
существует обратный элемент  , такой, что
, такой, что  .
.
Примеры.
3.1. Алгебра  есть поле, т.к.
есть поле, т.к.
1)  коммутативное кольцо;
коммутативное кольцо;
2)  ;
;
3) для любого  существует обратный элемент
существует обратный элемент 
3.2. Аналогично  ,
,  - поля.
- поля.
3.3. Коммутативное кольцо  полем не является, т.к. не выполняется условие 3.
полем не является, т.к. не выполняется условие 3.
3. 4. Коммутативное кольцо  является полем.
является полем.
3. 5. Множество матриц вида  образует поле относительно матричного сложения и умножения, а множество матриц
образует поле относительно матричного сложения и умножения, а множество матриц  полем не является, но является коммутативным кольцом с единицей.
полем не является, но является коммутативным кольцом с единицей.
Идеалы кольца
Пусть 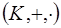 - коммутативное кольцо,
- коммутативное кольцо, 
Определение. Непустое подмножество J множества K называется идеалом кольца  , если:
, если:
1) 
2) 

 .
.
Теорема. Если J идеал кольца 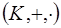 , то сложение и умножение – алгебраические операции в J, а алгебра
, то сложение и умножение – алгебраические операции в J, а алгебра  является подкольцом кольца
является подкольцом кольца  .
.
Примеры.
4.1. Пусть 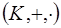 - произвольное кольцо, 0 – нулевой элемент этого кольца.
- произвольное кольцо, 0 – нулевой элемент этого кольца. 
1) 0-0=0, 
2)  тогда
тогда 
По определению идеала, множество  идеал данного кольца, называемый нулевым.
идеал данного кольца, называемый нулевым.
4.2. Пусть  - произвольное кольцо,
- произвольное кольцо,  .
.
1) 


 .
.
По определению идеала, множество  идеал кольца
идеал кольца 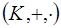 , называемый единичным идеалом.
, называемый единичным идеалом.
4.3. Пусть  - произвольное кольцо, m – фиксированный элемент данного кольца.
- произвольное кольцо, m – фиксированный элемент данного кольца. 

1) 
2) 



 .
.
По определению идеала, множество  идеал данного кольца. Он называется главным, порожденным элементом m, обозначается
идеал данного кольца. Он называется главным, порожденным элементом m, обозначается 
4.4. Пусть 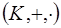 - произвольное кольцо;
- произвольное кольцо;  фиксированные элементы данного кольца.
фиксированные элементы данного кольца. 

Аналогично можно показать, что  идеал данного кольца. Он называется идеалом, порожденным элементами
идеал данного кольца. Он называется идеалом, порожденным элементами
 и обозначается символом J =(
и обозначается символом J =( .
.
 2020-04-12
2020-04-12 662
662








