Вычисление выборочного среднего


Вычисление выборочной дисперсии




Несмещенная оценка дисперсии




- теоретическое математическое ожидание


- теоретическая дисперсия
Построение доверительных интервалов для математического ожидания и дисперсии, соответствующих доверительной вероятности

- доверительная вероятность
Нахождение доверительного интервала для математического ожидания
Квантиль нормального распределения cо степенью свободы 334 и вероятностью


Границы доверительного интервала





Теоретическое значение параметра математического ожидания попадает в полученный доверительный интервал.
Нахождение доверительного интервала для дисперсии
Приближенное определение доверительного интервала для оценки дисперсии


Границы доверительного интервала





Теоретическое значение параметра дисперсии попадает в полученный доверительный интервал.
Проверка гипотезы о нормальном распределении случайной величины X, при использовании критерия Пирсона при уровне значимости
Первоначальное число интервалов группировки







Интервалы группировки



Определение частоты попадания выборочных значений в k-ый интервал




частоту попадания в каждый из интервалов нельзя назвать малой, поэтому объединение интервалов не требуется
Теоретическая вероятность попадания случайной величины X в интервал




Статистикой критерия Пирсона является величина


Заданный уровень значимости




- количество степеней свободы
=К-1, так как плотность вероятности теоретического распределения не зависит от неизвестных параметров, оцениваемых при выборке
Табличное значение статистики при уровне значимости =.1 и количестве степеней свободы =9



- условие не противоречивости гипотезы
Гипотеза принимается
Приложение 3
Параметры нормального закона распределения

- количество реализаций случайной величины
Объект управления
Параметры управления
Коэффициенты регулятора







- изменённая матрица В
Определение собственных значений измененной матрицы В




Действительные части собственных значений изменённой матрицы отрицательны, значит, система работает устойчиво
Определение собственных векторов матрицы


Определение матрицы собственных векторов и обратной её матрицы



Проверка


Получение выборочных значений случайной величины

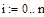

Генерирование ошибок измерений


Генерирование помех внутри объекта



Пересчет ошибок измерений в главную систему координат
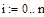





Пересчет помех в главную систему координат


Начальные условия


Пересчет начальных условий в главную систему координат


Интегрирование методом второго порядка точности

(при Т=2 процесс становится установившимся)






Пересчет из главной системы координат в исходную систему координат




Реализации случайного процесса


Значения переменных состояния в конечной точке





Определение статических характеристик системы управления в момент времени t=T
Вычисление выборочного среднего (математическое ожидание)
Вычисление выборочной дисперсии
функция XХ:
функция YY:




Корреляционный момент



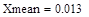


Оценка коэффициента корреляции


Проверка гипотезы о независимости переменных состояния системы в момент времени t=T
Анализ переменной состояния Х


Определение максимального и минимального значения выборки




Количество интервалов в гистограмме, определенное по правилу Стургерса


Длина интервала


Номер интервала

Выбираем точки Uk



Определение частоты попадания выборочных значений в k-ый интервал по переменной Х




Частота попадания в крайние интервалы достаточно мала, поэтому необходимо объединить крайние интервалы
Объединяем крайние интервалы












Рассмотри функцию Y


Определение максимального и минимального значения выборки




Количество интервалов в гистограмме, определенное по правилу Стургерса и также равно К
Номер интервала

Длина интервала





Определение частоты попадания выборочных значений в k-ый интервал по переменной Y
- частота попадания (Y)


Частота попадания в крайние интервалы достаточно мала, поэтому необходимо объединить крайние интервалы

Объединяем крайние интервалы







- частота попадания (Y)




Количество точек, попавших одновременно в оба интервала по двум переменным






- статистика


- уровень значимости


- количество степеней свободы


- табличное значение распределения (статистики) гипотеза принимается, если n<p

Гипотеза не принимается
 2020-04-12
2020-04-12 78
78








