
Решение:
Теоретический минимум
Рассмотрим линейное неоднородное дифференциальное уравнение(НЛДУ):

Функция  показывает, что уравнение неоднородное.
показывает, что уравнение неоднородное.
Если  , уравнение становится однородным (ОЛДУ).
, уравнение становится однородным (ОЛДУ).
Структура решения неоднородного линейного дифференциального уравнения:

Идея решения ОЛДУ состоит в том, что его ищут в виде  . Подставив это решение в ОЛДУ, получим
. Подставив это решение в ОЛДУ, получим
 – характеристическое уравнение.
– характеристическое уравнение.
Корни характеристического многочлена определяют вид решения линейного однородного дифференциального уравнения (Таблица 4).
Таблица 4 Решение линейного однородного дифференциального уравнения
| Корни характеристического уравнения | Вид общего решения ЛОДУ |
 - различные действительные корни - различные действительные корни
| 
|
 - корни кратности 2 (совпадают) - корни кратности 2 (совпадают)
| 
|
 - комплексно сопряженные корни - комплексно сопряженные корни
| 
|
Для нахождения частного решения неоднородного уравнения с правой частью специального вида:

необходимо воспользоваться таблицей 5.
Таблица 5 Решение НЛДУ с правой частью специального вида
| Правая часть ДУ | Характеристические корни ЛОДУ | Вид частного решения |
|
n,m – степени многочленов | Числа  не являются корнями характеристического уравнения не являются корнями характеристического уравнения
| 
|
Числа  являются корнями характеристического уравнения кратности r являются корнями характеристического уравнения кратности r
| 
| |
|
| Числа  не являются корнями характеристического уравнения не являются корнями характеристического уравнения
| 

|
Числа  являются корнями характеристического уравнения кратности r являются корнями характеристического уравнения кратности r
| 

| |
|
| Число  не являются корнями характеристического уравнения не являются корнями характеристического уравнения
| 
|
Число  являются корнями характеристического уравнения кратности r являются корнями характеристического уравнения кратности r
| 
| |
|
| Число 0 не являются корнями характеристического уравнения | 
|
| Число 0 являются корнями характеристического уравнения кратности r | 
|
________________________________________________
Нам дано неоднородное линейное дифференциальное уравнение

Его правая часть  может быть разбита на 2 слагаемых, каждое из которых будет представлять собой правую часть специального вида.
может быть разбита на 2 слагаемых, каждое из которых будет представлять собой правую часть специального вида.
Решим сначала соответствующее однородное дифференциальное уравнение: 
Составим характеристическое уравнение:  .
.
Тогда (см. табл.4) 
Рассмотрим два ЛНДУ с правыми частями специального вида:
 и
и 
1) Решим первое:  . (1)
. (1)
Согласно теореме о структуре решения НЛДУ необходимо найти частное решение данного неоднородного уравнения (см. табл.5).
Для  общий вид правой части:
общий вид правой части: 


 не совпадает с корнями характеристического уравнения.
не совпадает с корнями характеристического уравнения.
Тогда  .
.
Отсюда


Найдем неопределенные коэффициенты  подставив частное решение
подставив частное решение  в уравнение (1).
в уравнение (1).
Таблица 6 Подстановка частного решения с неопределенными коэффициентами

| 
|

| 
|
 = =
| 
|

| 
|
Приравняем коэффициенты при одинаковых выражениях в левой и правой частях равенства: 



Решив систему линейных уравнений

получим  .
.

Аналогично ищем частное решение уравнения для второй правой части специального вида:
2)  (2)
(2)
Для  общий вид правой части:
общий вид правой части: 
 совпадает с корнем характеристического многочлена дважды, поэтому:
совпадает с корнем характеристического многочлена дважды, поэтому:



Найдем неопределенный коэффициент  подставив частное решение
подставив частное решение  в уравнение (2).
в уравнение (2).

Приравняем коэффициенты при одинаковых выражениях в левой и правой частях равенства:



Значит, А=1.

Объединим все решения в одно:

Ответ: 
Задание 4.3.
Решить задачу Коши

Решение:
Теоретический минимум
________________________________________________
Решить задачу Коши – значит найти частное решение дифференциального уравнения, учитывая начальные условия.
От порядка дифференциального уравнения зависит, сколько произвольных констант будет в его общем решении.
одна произвольная константа. Для того чтобы найти ее значение необходимо одно начальное значение:  .
.
У дифференциальных уравнений второго порядка в общем решении две произвольные константы. Для решения задачи Коши нужно два начальныхусловия: 
При решении дифференциальных уравнений второго порядка, не являющихся линейными, применяют метод понижения порядка уравнения:
1) если в уравнении отсутствует переменная y:  , то рекомендуется замена:
, то рекомендуется замена:

2) если в уравнении отсутствует переменная x:  , то рекомендуется замена:
, то рекомендуется замена:

________________________________________________
Данное дифференциальное уравнение не является линейным и имеет второй порядок производной.
Решим его методом понижения порядка.
Уравнение не содержит переменной х, поэтому заменим  на новую переменную, зависящую от у.
на новую переменную, зависящую от у.

 (*)
(*)
I Случай.
Если y  , то подставив его в исходное уравнение, получим верное равенство. Значит, y
, то подставив его в исходное уравнение, получим верное равенство. Значит, y  – особое решение уравнения.
– особое решение уравнения.
II Случай.
Если y  , то разделим на
, то разделим на  уравнение (*).
уравнение (*).

Получили уравнение вида 
Это уравнение Бернулли.
Оно решается с помощью подстановки 

Идея решения данного уравнения с двумя неизвестными функциями заключается в сведении его к системе из двух уравнений.
Предположим, что

тогда

0
Получим систему 
Решим первое уравнение системы.

1) Если  , то это означает, что
, то это означает, что  . Так как
. Так как  , то
, то  . Подставляя константу в исходное уравнение
. Подставляя константу в исходное уравнение  , получим, что
, получим, что  . Но мы рассматриваем случай y
. Но мы рассматриваем случай y  . Получили противоречие.
. Получили противоречие.
2)  ,
, 


Подставляем решение первого уравнения системы во второе:


Получим  Учтем, что
Учтем, что 
Используем начальные условия, чтобы найти  .
.


Итак,


Подставим начальные условия, чтобы найти  .
.

Таким образом, получили ответ:

Вариант 1
1. Дано комплексное число 
Требуется:
1.1) записать число а в алгебраической, тригонометрической и показательной формах;
1.2) найти все корни уравнения 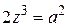 и изобразить их на комплексной плоскости.
и изобразить их на комплексной плоскости.
 2020-04-07
2020-04-07 123
123


 и
и  .
. , причем степень многочленов может быть и нулевой, то есть они представляют из себя некоторые числовые константы
, причем степень многочленов может быть и нулевой, то есть они представляют из себя некоторые числовые константы








