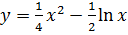 на отрезке [1,e].
на отрезке [1,e].
Решение:
Теоретический минимум
________________________________________________
С помощью определенного интеграла можно найти длину дуги (рис. 8), заданной функцией, как в явном, так и в параметрическом виде, а также в полярной системе координат.

Рис. 8
1. В декартовых координатах: 
2. В полярных координатах: r 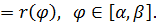
3. Параметрически: x 

1. В декартовых координатах: 
2. В полярных координатах: 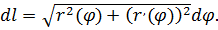
3. Параметрически: 
В случае параметрической функции и функции в полярной системе координат в пределах интегрирования стоят соответственно  .
.
В нашем случае



Ответ: длина дуги равна 
Задание 3.3.
Определить, сходится ли данный интеграл. Если сходится, то к какому числу.

Решение:
Теоретический минимум
________________________________________________
Пусть функция  непрерывна на интервале
непрерывна на интервале  Тогда она будет непрерывна на любом интервале
Тогда она будет непрерывна на любом интервале  где
где  и существует интеграл
и существует интеграл 
Несобственным интегралом 1-го рода называется интеграл, определяемый равенством 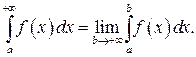
Если соответствующий предел существует и конечен, то говорят, что несобственный интеграл 1-го рода сходится, иначе несобственный интеграл называют расходящимся.
Аналогично, если функция  непрерывна на промежутке интегрирования, то интегралы вида
непрерывна на промежутке интегрирования, то интегралы вида 
 также являются несобственными интегралами1-го рода.
также являются несобственными интегралами1-го рода.
________________________________________________
Интеграл

Имеет неограниченный верхний предел интегрирования. Внутри полуинтервала  подынтегральная функция
подынтегральная функция  непрерывна. Значит, перед нами несобственный интеграл 1 рода.
непрерывна. Значит, перед нами несобственный интеграл 1 рода.

Решим отдельно соответствующий неопределенный интеграл, а затем - подставим пределы интегрирования.
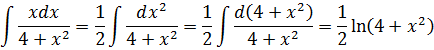

Интеграл не равен конечному числу, значит, он расходится.
Задание 4.1.
 2020-04-07
2020-04-07 112
112








