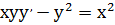 .
.
Решение:
Теоретический минимум
________________________________________________
Рассмотрим основные понятия теории дифференциальных уравнений.
Уравнения, связывающие независимую переменную, искомую функцию и ее производные или дифференциалы, называются дифференциальными.
Порядок дифференциального уравнения – это порядок старшей производной, входящей в дифференциальное уравнение.
Таким образом, дифференциальное уравнение первого порядка можно записать в виде 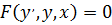 .
.
Аналогично, дифференциальное уравнение второго порядка можно записать в виде 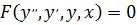 .
.
Решить дифференциальное уравнение - значит найти такую непрерывную дифференцируемую n раз функцию 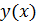 , которая при подстановке в это уравнение превращает его в верное равенство (n – это порядок дифференциального уравнения).
, которая при подстановке в это уравнение превращает его в верное равенство (n – это порядок дифференциального уравнения).
Среди дифференциальных уравнений первого порядка рассмотрим уравнения с разделяющимися переменными, однородные, линейные и уравнения Бернулли (Таблица 3).
Таблица 3. Решение ДУ первого порядка
| № | Название ДУ | Вид ДУ | Схема решения ДУ |
| 1 | Уравнение с разделяющимися переменными | 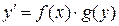 или
или
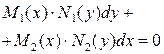
| Разделяем переменные
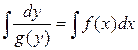 и интегрируем обе части уравнения.
и интегрируем обе части уравнения.
|
| 2 | Однородное | 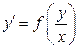 или или 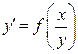
| Подстановка 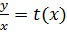 приводит уравнение к уравнению с разделяющимися переменными. приводит уравнение к уравнению с разделяющимися переменными.
|
| 3 | Линейное | 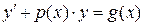
| Подстановка Бернулли 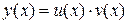 , приводит исходное уравнение к виду: , приводит исходное уравнение к виду: 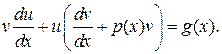 Из условия Из условия 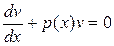 находим находим 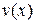 , подставляем в уравнение , подставляем в уравнение 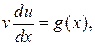 получаем получаем 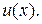
|
| 4 | Уравнение Бернулли | 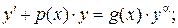
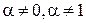
| Подстановка Бернулли 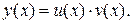
|
________________________________________________
Уравнение 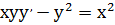 является однородным дифференциальным уравнением первого порядка.
является однородным дифференциальным уравнением первого порядка.
Действительно, разделив обе его части на xy получим:
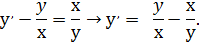
Сделаем замену:
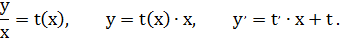
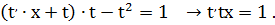
Однородное уравнение свелось к дифференциальному уравнению с разделенными переменными.
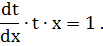
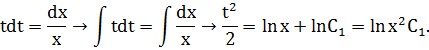
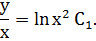
Задание 4.2.
 2020-04-07
2020-04-07 287
287








