Б). Случай непрерывного спектра

 

.

1. Собственные функции, принадлежащие различным собственным значениям эрмитового оператора, ортогональны:

                   .          (6.7)
Здесь предполагается, что .

Если , то для собственных функций 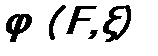 будет условие нормировки. Однако возникает проблема – нормировочный интеграл расходится.

                      .         (6.8)

Причина – нельзя в непрерывном спектре брать точное значение F, необходимо рассматривать бесконечно малый интервал значений F, F+dF. При этом собственную функцию 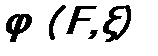 надо заменять «волновым пакетом»  :

.

Тогда нормировочный интеграл расходиться не будет:

,

и можно вместо функций 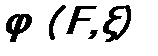 пользоваться волновыми пакетами. Однако на практике их использование сильно усложняет математический аппарат квантовой механики. Тем не менее, как показал П. Дирак, все же можно сохранить собственные функции 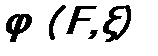, но только изменить условие их нормировки, а именно, заменить соотношения (32) и (33) единым:

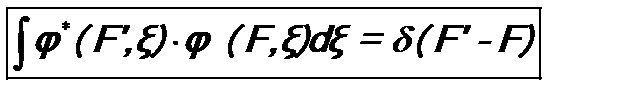       .     (6.9)

Это условие ортонормировки собственных функций оператора с непрерывным спектром. Принято говорить, что для непрерывного спектра собственные функции должны быть нормированы на дельта-функцию Дирака.

 

2. Система собственных функций полная.

Как и раньше, это означает, что произвольная функция Ψ (ξ), удовлетворяющая стандартным условиям, можно быть представлена в виде интегрального разложения по собственным функциям :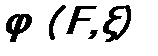

          .        (6.10)

Для нахождения коэффициентов разложения a(F) умножим соотношение (6.10) на   и проинтегрируем по ξ:

Мы использовали нормировочное соотношение (6.9) и свойство 3 дельта-функции Дирака. Получаем:

             .        (6.11)

Если функция Ψ (ξ) нормирована, то, подставив в условие ее нормировки разложение (6.10), можно получить его критерий полноты этого разложения:

                  .                   (6.12)

3. Условие полноты системы собственных функций

Оно имеет вид (сравни с (6.6):

                       .  (6.13)

Из-за важности свойств собственных функций операторов для практических приложений математического аппарата квантовой механики суммируем эти свойства в виде таблицы.

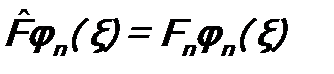
Случай дискретного  спектра	Случай непрерывного  спектра
1.Условие ортонормировки	1.Условие ортонормировки
2.Свойство полноты	2.Свойство полноты
3.Условие полноты	3.Условие полноты

 Из сравнения формул двух столбцов видно, что свойства аналогичны, если делать замены:

n   F, φ_n(ξ)   φ(F,ξ),  , δ_mn   δ(F’-F).

Отметим еще важное свойство собственных функций двух операторов. Пусть есть два линейных эрмитовых оператора ,  и известны решения их уравнений на

собственные функции и собственные значения:

 и .

Тогда можно доказать два свойства:

1. Если операторы  и   коммутируют,

т.е. , то у них будет общая система собственных функций: .

2. Если у операторов  и   общая система собственных функций, т.е. , то они коммутируют: ۰ = ۰ .  

Лекция 7

ОСНОВНЫЕ ПОСТУЛАТЫ КВАНТОВОЙ МЕХАНИКИ