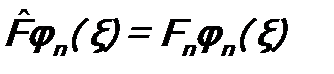
1. Собственные функции, принадлежащие различным собственным значениям эрмитового оператора, ортогональны.
Докажем. Пусть собственная функция φn (ξ) принадлежит собственному значению Fn, а собственная функция φm (ξ) → Fm, причем Fn 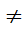 Fm.
Fm.  Это означает, что удовлетворяются уравнения:
Это означает, что удовлетворяются уравнения:
 , (a)
, (a)
 . (b)
. (b)
Умножим справа уравнение (a) на φm* (ξ), уравнение (b) заменим на комплексно ему сопряженное и умножим его справа на φn (ξ). Получим
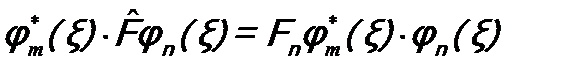 ;
;
 .
.
Во втором уравнении учтено, что Fm = Fm *, как было доказано выше. Проинтегрируем эти равенства по всему пространству и вычтем одно из другого.
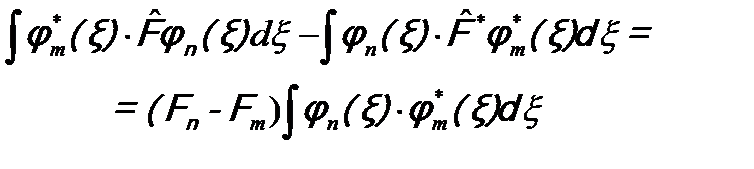 .
.
Из условия эрмитовости оператора 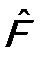 (см. (5.7)) следует:
(см. (5.7)) следует:  .
.
Тогда  .
.
Так как по условию Fn 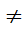 Fm, то
Fm, то
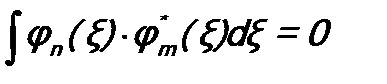 , (c)
, (c)
что и требовалось доказать. Обычно собственные функции оператора нормируют. Поэтому
 . (d)
. (d)
Объединяя условия (c) и (d) в одно, получим условие ортонормировки собственных функций:
 . (6.1)
. (6.1)
Здесь  - символ Кронекера:
- символ Кронекера:
 . (6.2)
. (6.2)
Аналогично условие ортонормировки можно записать и для собственных функций оператора с вырожденным спектром (см. (5.10) ):
 .
.
2. Система собственных функций линейного эрмитового оператора полная.
Это свойство означает, что произвольную функцию Ψ (ξ), удовлетворяющую стандартным условиям, можно разложить в ряд по собственным функциям линейного эрмитового оператора φn (ξ):
 . (6.3)
. (6.3)
Коэффициенты разложения an можно найти, умножив соотношение (6.3) на φm* (ξ) и проинтегрировав по ξ:
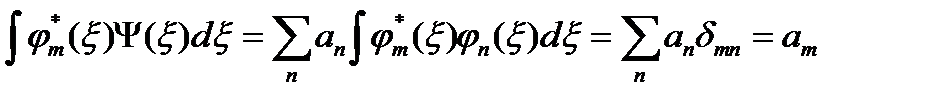 .
.
Здесь было использовано условие ортонормировки собственных функций (6.1) и определение символа Кронекера (6.2). Таким образом,
 . (6.4)
. (6.4)
Если функция Ψ (ξ) нормирована, то, подставив
в условие ее нормировки разложение (6.3), можно для коэффициентов an получить критерий полноты разложения (6.3):
 . (6.5)
. (6.5)
3. Условие полноты системы собственных функций
 . (6.6)
. (6.6)
Здесь ξ и ξ’ – две пространственных точки.
δ (ξ) – дельта-функция Дирака. Поскольку она часто используется в квантовой механике, отметим некоторые ее свойства.
1.  ;
;
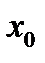 - фиксированная координата в пространстве.
- фиксированная координата в пространстве.
2.  .
.
Точки a и b задают интервал интегрирования [ a, b ].
3.  .
.
 - произвольная функция.
- произвольная функция.
4. 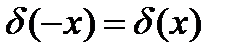 .
.
5.  .
.
6.  ;
;
7. 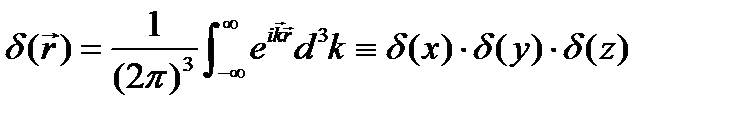 .
.
8. 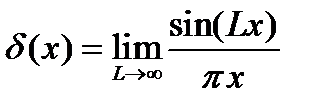 ;
;  .
.
 2020-04-12
2020-04-12 280
280








