Задача 1. Построить СДНФ,СКНФ и ПЖ функции 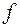 .
.
Существуют два вида алгоритмов посроения СДНФ, СКНФ и ПЖ. Это алгоритмы, основанные на построении таблиц истинности,с одной стороны, и алгоритмы, состоящие в эквивалентном преобразовании формул к заданному специальному виду, с другой.
Алгоритм построения СДНФ (с использованием таблиц истинности):
- построить таблицу истинности данной функции 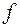 ;
;
- в таблице выделить наборы, на которых функция принимает значение 1;
- каждому такому набору 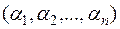 поставить в соответствие элементарную конъюнкцию
поставить в соответствие элементарную конъюнкцию
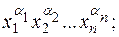 (7)
(7)
- найденные элементарные конъюнкции объединить знаком дизъюнкции, - полученная формула, согласно теореме 1, является совершенной дизъюнктивной нормальной формой функции f.
Алгоритм построения СКНФ (c использованием таблиц истинности):
- построить таблицу истинности данной функции 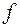 ;
;
- в таблице выделить наборы, на которых функция принимает значение 0;
- каждому такому набору 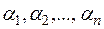 поставить в соответствие элементарную дизъюнкцию вида:
поставить в соответствие элементарную дизъюнкцию вида:
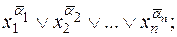 (8)
(8)
- найденные элементарные дизъюнкции объединить знаком конъюнкции, - полученная формула, согласно теореме 2, является совершенной конъюнктивной нормальной формой функции 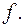
Алгоритм построения ПЖ (метод неопределенных коэффициентов):
- построить таблицу истинности данной функции 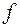 ;
;
- записать общий вид полинома Жегалкина. В случае трех переменных имеем:
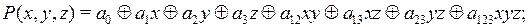 (9)
(9)
- исходя из того, что данная функция 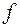 и ее ПЖ принимают одинаковые значения на всевозможных наборах переменных, в них входящих, составим систему уравнений для коэффициентов
и ее ПЖ принимают одинаковые значения на всевозможных наборах переменных, в них входящих, составим систему уравнений для коэффициентов 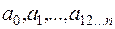 . В случае трех переменных имеем:
. В случае трех переменных имеем:
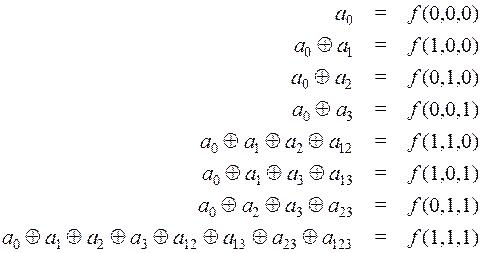
Решаем эту систему "сверху вниз"; найденные коэффициенты 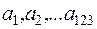 подставляем формулу (9) и получаем ПЖ заданной функции
подставляем формулу (9) и получаем ПЖ заданной функции 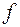 .
.
Алгоритмы построения СДНФ, СКНФ и ПЖ с помощьюэквивалентных преобразований:
Построение СДНФ и СКНФ при помощи эквивалентных преобразований можно разбить на следующие этапы:
- выразить логические операции 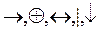 через
через 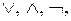 используя равносильности:
используя равносильности:
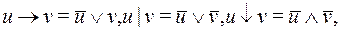 (10)
(10)
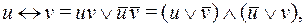 (11)
(11)
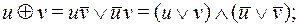 (12)
(12)
- используя законы де-Моргана, добиться того, чтобы знак отрицания стоял только над элементарными высказываниями:
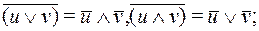 (13)
(13)
- для упрощения преобразований использовать закон двойного отрицания, законы идемпотентности и законы поглощения и склеивания:
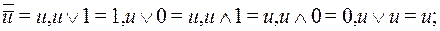 (14)
(14)
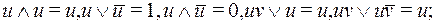 (15)
(15)
- при построении СДНФ (СКНФ) преобразовать полученное ранее выражение в ДНФ (КНФ), используя первый (второй) дистрибутивные законы:
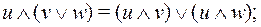 (16)
(16)
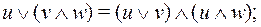 (17)
(17)
если в полученной ДНФ (КНФ) какое-либо слагаемое 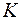 (сомножитель
(сомножитель 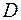 ) не содержат переменной
) не содержат переменной 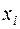 , от которой зависит данная функция, то нужно произвести эквивалентную замену:
, от которой зависит данная функция, то нужно произвести эквивалентную замену: 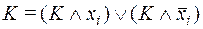 для ДНФ и
для ДНФ и 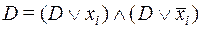 для КНФ; в полученном выражении из нескольких одинаковых слагаемых (сомножителей) оставить только одно (один), так как
для КНФ; в полученном выражении из нескольких одинаковых слагаемых (сомножителей) оставить только одно (один), так как 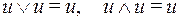 .
.
При построении ПЖ предварительно выразим данную функцию через 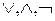 при помощи равносильностей (10) -(13). Далее выразим
при помощи равносильностей (10) -(13). Далее выразим 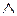 через
через 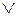 и
и 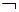 :
:
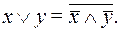 (18)
(18)
В полученном выражении проведем преобразования, выразив операцию 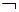 через
через 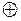 :
: 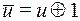 , - и, раскрыв скобки:
, - и, раскрыв скобки: 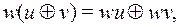 удалим лишние слагаемые, так как
удалим лишние слагаемые, так как 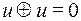 .
.
С изложенным здесь понятиями и фактами можно познакомиться в [1], стр. 19-23 и [2], стр. 24-54.
 2020-04-12
2020-04-12 150
150








