Обозначим через Б множество всех булевых функций.
Определение 5. Замыканием множества 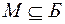 называется множество суперпозиций, которые можно построить из функций
называется множество суперпозиций, которые можно построить из функций  . С понятием суперпозиции можно познакомиться в [1], стр. 50, [4], стр. 22.
. С понятием суперпозиции можно познакомиться в [1], стр. 50, [4], стр. 22.
Определение 6. Класс (множество) булевых функций называется замкнутым, если он совпадает со своим замыканием.
Определение 7. Система (множество) булевых функций называется полной в Б, если ее замыкание совпадает с множеством всех булевых функций.
Определение 8. Система (множество) булевых функций называется базисом, если она полна и любая ее подсистема не является полной в 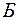 .
.
Основные замкнутые классы:
1) класс 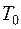 функций, сохраняющих константу 0:
функций, сохраняющих константу 0:
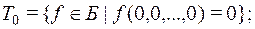
2) класс 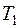 функций, сохраняющих константу 1:
функций, сохраняющих константу 1:
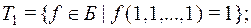
3) класс 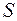 самодвойственных функций:
самодвойственных функций:
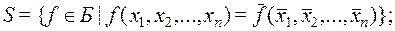
4) класс  монотонных функций:
монотонных функций:
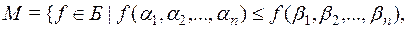
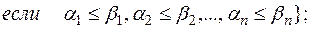
5) класс 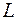 линейных функций:
линейных функций:
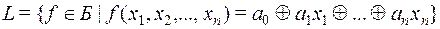
Теорема 4. (Критерий ПОСТА). Для того, чтобы система булевых функций 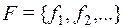 была полной в
была полной в 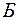 , необходимо и достаточно, чтобы она целиком не содержалась ни в одном из замкнутых классов
, необходимо и достаточно, чтобы она целиком не содержалась ни в одном из замкнутых классов 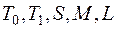 .
.
 2020-04-12
2020-04-12 94
94








