Порядок выполнения домашнего задания

Примеры решения задач

Пример 1.1. Построить СДНФ, СКНФ и ПЖ для функции  c использованием таблицы истинности.

 

Построим таблицу истинности для данной функции:

                       

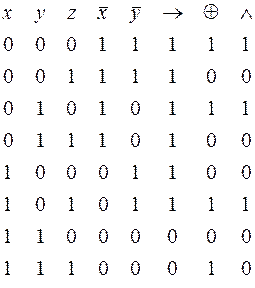
Из построенной таблицы следует, что функция принимает значение 1 на наборах: (0,0,0), (0,1,0), (1,0,1), -- которым соответствуют элементарные конъюнкции: 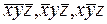, дизъюнкция этих конъюнкций есть СДНФ данной функции:

                          

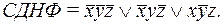
Для построения СКНФ выделим те наборы, на которых функция принимает значение 0: (0,0,1), (0,1,1), (1,0,0), (1,1,0), (1,1,1). Им соответствуют элементарные дизъюнкции: 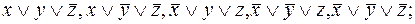 конъюнкция этих дизъюнкций является СКНФ данной функции:

                  

               

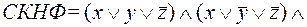
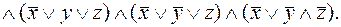
Для построения полинома Жегалкина используем его преставление (9). Составим систему уравнений для неизвестных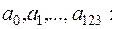  

      

 

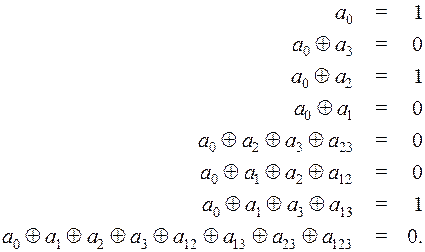
Решая эту систему уравнений "сверху вниз", находим: 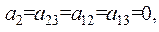 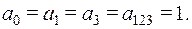Подставляя найденные коэффициенты в (9), получим

                         

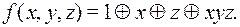
Пример 1.2 Построить СДНФ,СКНФ И ПЖ для функции

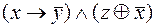 методом эквивалентных преобразований.

 

             

 

          

 

        

            

 

         

 

                           

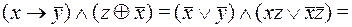
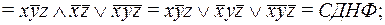
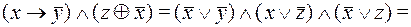
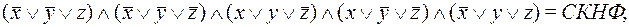
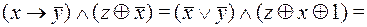
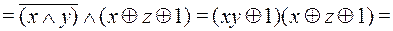
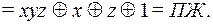
Cравнивая результаты, полученные в прмерах 1 и 2, читатель еще раз может убедиться в единственности представления формулы в виде СДНФ, СКНФ и ПЖ.

 

Задачи для самостоятельного решения

Задача 1. Построить СДНФ, СКНФ и ПЖ для следующих формул алгебры высказываний.

 1)

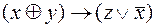
2)

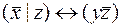
3)

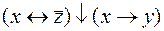
4)

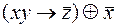
5)

6)

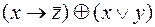
7)

 

Домашнее задание №2, 3.

Замкнутость и полнота. Основные замкнутые классы. Критерий Поста. Построение базиса