2020-04-12
131
110 – АТПП 30.03.2020 г.
120 – ГХ 01.04.2020г.
139 – ПО 30.03.2020 г.
Вариант 1
1. Точка движется прямолинейно по закону
 Найти скорость и ускорение точки в момент времени  .
2. Точка движется прямолинейно по закону
 Определить момент времени, когда ускорение тела будет
равным 0.
3. Найти производную второго порядка
а) 
б) 
в) 
| Вариант 2
1. Точка движется прямолинейно по закону  Найти скорость и ускорение точки в момент времени  .
2. Два тела движутся прямолинейно по законам  и  Определить момент времени, когда скорости этих тел будут равны.
3. Найти производную второго порядка
а) 
б) 
в) 
|
Вариант 3
1. Точка движется прямолинейно по закону
 Найти скорость и ускорение точки в момент времени  .
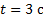2. Точка движется прямолинейно по закону
 Определить моменты времени, когда скорость тела будет
равна 0.
3. Найти производную второго порядка
а) 
б) 
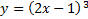в) 
| Вариант 4
1. Точка движется прямолинейно по закону
 Найти скорость и ускорение точки в момент времени .
2. Два тела движутся прямолинейно по
законам  и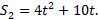 
Определить момент времени, когда скорости
этих тел будут равны.
3. Найти производную второго порядка
а)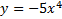 
б) 
в) 
|
Вариант 5
1. Точка движется прямолинейно по закону
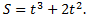 Найти скорость и ускорение точки в момент времени .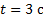
2. Закон движения частицы определяется уравнением 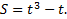 Каково ускорение частицы в момент, когда её скорость равна  .
3. Найти производную второго порядка
а) 
б) 
в) 
| Вариант 6
1. Точка движется прямолинейно по закону
 Найти скорость и ускорение точки в момент времени  .
2. Для машины тормозной путь определяется
формулой  В течении какого времени осуществляется торможение до полной остановки.
3. Найти производную второго порядка
а) 
б) 
в) 
|
Лекция
Геометрический смысл производной.
Тангенс угла наклона касательной (угловой коэффициент наклона касательной), проведенной к графику функции 
в точке 
равен производной функции в этой точке:
Заметим, что угол α - это угол между прямой и положительным направлением оси ОХ.
Что самое важное нужно знать о прямой на координатной плоскости? Поскольку прямая – это изображение линейной функции, очень удобно было бы знать ее уравнение. То есть коэффициенты k и b в уравнении
Но ведь k мы уже знаем! Это угловой коэффициент касательной, который равен производной функции в этой точке 
Рис. 1
Теперь остается найти b. Это проще простого: b значение 
при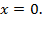 
Графически 
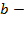это координата пересечения прямой с осью ординат. Рассмотрим рис.1, проведём ВС параллельно оси Ох, очевидно, что треугольник АВС прямоугольный, 
, 
, выразим b:
Соберём полученные данные:
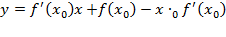
Уравнение касательной к графику функции 
в точке x0 имеет вид:
!
В этом уравнении:
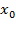- абсцисса точки касания,
- значение функции y=f(x) в точке касания,
- значение производной функции y=f(x) в точке касания.
Пример:
Найти уравнение касательной к графику функции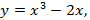 
в точке 
.
Алгоритм решения:!
1.Вычислим 
2. Найдём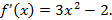 
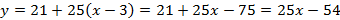
4. Подставим, полученные данные в уравнение касательной:
уравнение касательной.
Практика (Самостоятельно):
Найти уравнение касательной
1. 
2. 
.
3. 
.
4. 
Нормаль - это прямая, проходящая через точку касания к графику функции перпендикулярно касательной.
!
Пример: Найти уравнения касательной и нормали к графику функции 
, в точке 
Алгоритм решения:!
1. 
2. f′(x)= 
.(производная)
3. 
.
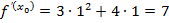4. Подставим, полученные данные в уравнение касательной, и нормали
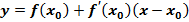
Касательная: 
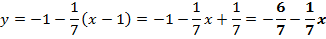
Нормаль: 
Примечание:
1. Угловые коэффициенты параллельных прямых равны, т.е. если прямые 
и 
параллельны, то 
.
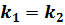2. Угловые коэффициенты перпендикулярных прямых взаимно обратны и противоположны по знаку, т.е. если прямые и перпендикулярны, то 
.
Составить самостоятельно уравнения касательной и нормали к графику функции:
1. 
в точке 
2. 
в точке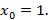 
3. 
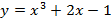в точке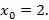 
4. 
в точке 
