Аналитическое решение

Опишем плотность вероятности 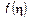 погрешностей емкости конденсаторов математическим выражением. Так как по определению площадь под кривой плотности, в нашем случае площадь треугольника, должна равняться единице, т. е.

,

то максимальное значение плотности

.

При этом крутизна функции плотности левой ее части будет равна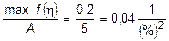

и правой части .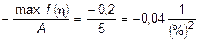

Следовательно, плотность вероятности определится следующей функцией:

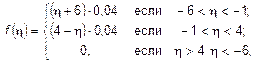
где все числовые значения выражены в процентах.

Вероятность того, что случайная величина 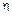 попадает в интервал [ a; b ], по определению равна

P { a < 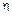  £ b } = .

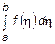Из условия задачи следует, что a = –1%, b = 1%. Так как интервал [–1;1] находится внутри интервала [–1;4], искомая вероятность для первой группы равна:

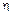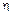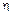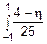P {–1 <  £ 1} = f () d  =  dx =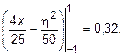

События {| 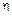  | £ 1%} и {|  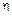 |> 1%} противоположны, тогда

P {| 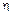|£1} + P {|  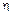 |>1} = 1.

Следовательно, вероятность того, что конденсатор попадет во вторую группу, равна P {| 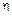  |>1} = 1– P {|  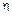 |£ 1} = 1 – 0,32 = 0,68.

Таким образом, в первую группу попадает в среднем 32% конденсаторов, а во вторую – 68%.

Графоаналитическое решение

По заданным условиям построим в соответствующем масштабе плотность вероятностей f (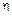)погрешности емкости конденсаторов (рисунок 4.1).

Границы групп разбраковки обозначены D (–1%) и F (+1%).

Рисунок 4.1 – Треугольная плотность вероятности погрешности
емкости конденсаторов

Вероятность попадания конденсатора в первую группу равна заштрихованной площади, которую можно вычислить как разность площадей:

Р {| 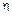  |£ 1 } = S_BDC – S_EFC =

= ,

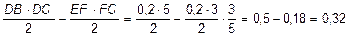так как EF = 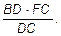 Следовательно, вне допуска окажется 0,68 части от всей партии, т. е. 68%.

Задача 4.2