Минимальный зазор равен разности предельных размеров или нижнего отклонения отверстия и верхнего отклонения вала

S _min = D _min – d _max= EI – es = 0 мкм.

Средний зазор

m_S =  = 13,5 мкм.

3 Изобразим схему полей допусков и укажем основные характеристики посадки с зазором (рисунок 4.2).

Рисунок 4.2 – Схема полей допусков посадки с зазором Æ50

4 Определим среднее отклонение отверстия и вала

E _m =  мкм,

e _m = 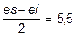мкм.

5 Погрешности изготовления диаметров вала и отверстия независимы, поэтому среднее квадратическое отклонение зазора в соединении

мкм.

6 Нормированная нормально распределенная случайная величина Z в границах поля допуска принимает значение

z _min =

z _max =

7 Определим вероятность выполнения требований посадки с помощью функции Лапласа

Р = Ф(z _max) – Ф(z _min) = 0,968

Вероятности недопустимого зазора и натяга будут равны

P _нед = =1,6 %.

8 График распределения плотности вероятности представлен на рисунке 4.3. Заштрихованные области показывают вероятности недопустимого зазора в соединении и возникновения натяга.

Рисунок 4.3 – График распределения плотности вероятности

Задача 4.3

Оценивание доли годных изделий при нормальном распределении погрешности технологического процесса

Автомат изготовляет шарики для подшипников. Номинальный диаметр шариков D _ном = 10 мм. Вследствие неточности изготовления фактический диаметр шарика является случайной величиной, распределенной по нормальному закону с математическим ожиданием m = 10,02 мм и средним квадратическим отклонением s = 0,04 мм.

При контроле бракуются все шарики, диаметр которых отличается от номинального более чем на 0,1 мм.

Определить, какой процент шариков в среднем будет отбраковываться.

 

Решение

 

Границы интервала допустимых значений диаметра шарика

а = 10 – 0,1 = 9,9 мм и b = 10 + 0,1 = 10,1 мм.

Вероятность того, что шарик не будет забракован, равна

P (a £ D £ b) = F (b) – F (a),

где F – значения функций распределения случайной величины D при D = b и D = a соответственно. Воспользуемся табулированным интегралом Лапласа–Гаусса для нормального распределения Ф₀(z), где
  z =  – нормированная центрированная случайная величина
 (х – случайная величина в общем случае, здесь х = D). Тогда:

F (b) – F (a) = Ф₀  – Ф₀ 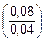 = Ф₀  – Ф₀  =

= Ф(2) – Ф(–3) = Ф(2) + Ф(3) = 0,4772 + 0,4986 – 1» 0,976.

Поскольку Р [ D < a; D > b ] = 1 – Р (a £ D £ b), искомая вероятность будет равна 1–0,976 = 0,024 или 2,4%, т. е. в среднем именно такой процент шариков будет отбраковываться.

 

Задача 4.4