|
Пусть U=U(x) и V=V(x) – дифференцируемые функции. По свойству дифференциала d(U·V)=VdU+UdV UdV=d(U·V)-VdU.
Интегрируем обе части равенства: 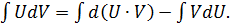
Используя свойства неопределенного интеграла, получаем формулу интегрирования по частям для неопределенного интеграла:
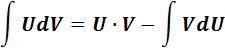
|
При её применении фиксируется разбиение подынтегрального выражения искомого интеграла на два сомножителя U и dV. При переходе к правой части формулы первый из сомножителей дифференцируется (при нахождении дифференциала dU=U´dx), второй интегрируется (V= 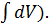
Возможности применения формулы интегрирования по частям связаны с тем, что дифференцирование может существенно упростить один из сомножителей (при условии, что интегрирование не слишком усложнит другой).
Пример 1. 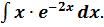
Так как x´=1, а 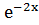 при интегрировании практически не изменяется (появляется лишь постоянный множитель
при интегрировании практически не изменяется (появляется лишь постоянный множитель 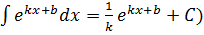 , то данный интеграл можно найти интегрированием по частям.
, то данный интеграл можно найти интегрированием по частям.
Пусть U=x; dV= 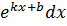 , тогда dU=dx;
, тогда dU=dx; 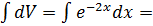 k=-2; b=0 =-
k=-2; b=0 =- 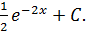
Применяя формулу интегрирования по частям, получаем:
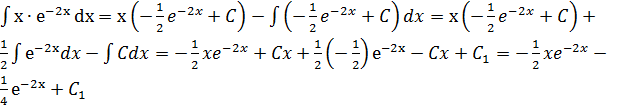
Замечание: Анализ полученного решения показывает, что постоянная С, возникшая при нахождении V (по заданному dV), не входит в запись окончательного ответа. Аналогично, в общем случае постоянная С, возникшая при нахождении V, исключается в процессе решения. Поэтому в дальнейшем, применяя формулу интегрирования по частям и найдя V, будем полагать С=0, что несколько упрощает запись решения.
Пример 2. 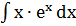 .
.
Пусть U=x; dV= 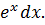
Тогда dU=dx; V= 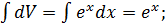
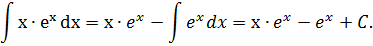
Пример 3. 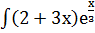 dx.
dx.
Пусть U=2+3x; dV= 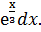
Тогда dU=d(2+3x)=(2+3x)´dx=3dx; V= 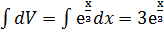 .
.
Применяя формулу интегрирования по частям, получаем:
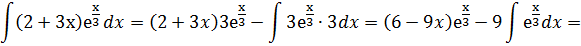
= 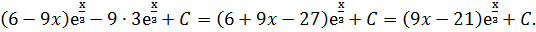
Пример 4. 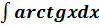
U dV
Пусть arctgx=U; dx=dV
Тогда dU=(arctgx)´dx= 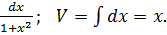
Получаем согласно формулы интегрирования по частям:
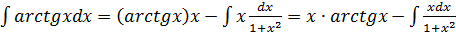 =
=
= 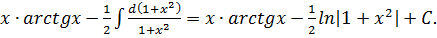
Указание. Все интегралы, которые находят с использованием формулы интегрирования по частям, можно разбить на три группы.
I группа: 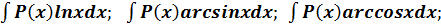
 , где P(x) –многочлен.
, где P(x) –многочлен.
В данной группе полагаем U=lnx; U=arcsinx; U=arccosx; U=artgx; U=arcctgx, а оставшееся выражение за dV=P(x)dx.
II группа: 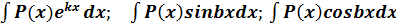 , где Р(х)- многочлен, k и b-числа.
, где Р(х)- многочлен, k и b-числа.
В данной группе полагаем U=P(x), а оставшееся выражение за dV.
III группа: 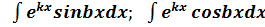 .
.
Эта группа сложных интегралов. Они находятся при помощи двукратного интегрирования.
Пример 5. 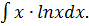
Пусть U=lnx; dV=xdx.
Тогда dU=d(lnx)= 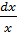 ; V=
; V= 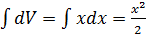 .
.
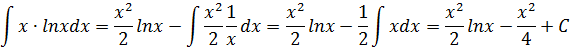
Пример 6. 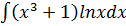 .
.
Пусть U=lnx; dV= 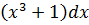 .
.
Тогда dU=d(lnx)= 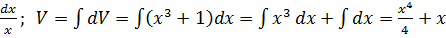 .
.
Применяя формулу интегрирования по частям, получаем:
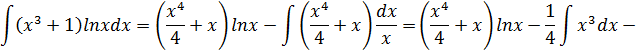
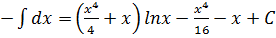 .
.
 2020-04-12
2020-04-12 170
170








