Пример 7.  .
.
Пусть U= 
Тогда dU=d(
Применяя формулу интегрирования по частям, получаем:

Так как многочлен второй степени, то в результате однократного интегрирования степень его понизилась на единицу, поэтому получившийся интеграл мы должны еще раз проинтегрировать, чтобы он уничтожился и остался табличный интеграл.
Пусть U=x; dV=cosxdx.
Тогда dU=dx; V= 
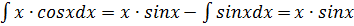 +cosx+C.
+cosx+C.
Подставляя полученный результат в первоначальный интеграл, имеем:

Пример 8.  .
.
Этот интеграл относится к третьей группе интегралов.
Пусть U=cosx; dV= 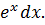
Тогда dU=-sinxdx; V= 

Рассмотрим 
Пусть U=sinx; dV= 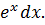
Тогда dU=cosxdx; V= 

Подставим найденное значение в (1):
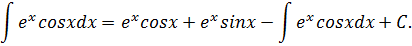
Переносим  из правой части в левую с противоположным знаком, получим: 2
из правой части в левую с противоположным знаком, получим: 2  Из полученного уравнения находим чему равен искомый интеграл, поделив обе части равенства на 2.
Из полученного уравнения находим чему равен искомый интеграл, поделив обе части равенства на 2.

Задание №17.
| № | ЗАДАНИЕ | ОТВЕТ |
| 1. | 
| 
|
| 2. | 
| (x-1)cosx-sinx+C |
| 3. | 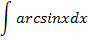
| x·arcsinx+ 
|
| 4. | 
| 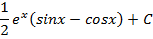
|
ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
1. 
4. 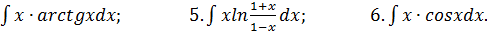
УКАЗАНИЯ К ОТВЕТАМ
Задание №1
| № п/п | № ответа | Пояснения |
| 1. | 1. | 2 как постоянный множитель нужно вынести за знак интеграла (свойство1) и только после этого интегрировать. |
| 2. | Забыли С. | |
| 3. | Верно. | |
| 4. | Дифференцируете функцию, а не интегрируете. | |
| 5. | Функция вынесена за знак интеграла, а не проинтегрирована, см. 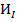 . .
| |
| 2. | 1. | Интеграл от произведения двух функций не равен произведению этих функций. Нужно предварительно раскрыть скобки в подынтегральном выражении и воспользоваться свойствами 3 и 4, и  . .
|
| 2. | Верно. | |
| 3. | Забыли С. См. определение интеграла. | |
| 4. | Неверно применили  , показатель степени и знаменатель равные (n+1), а не n. , показатель степени и знаменатель равные (n+1), а не n.
| |
| 5. | Неверно применили  Деление на степень не сделали. Деление на степень не сделали.
| |
| 3. | 1. | Верно. |
| 2. | Забыли С. | |
| 3. | Интеграл дроби не равен отношению интеграла числителя к интегралу знаменателя. Подынтегральное выражение нужно предварительно преобразовать. См.  , пример 3. , пример 3.
| |
| 4. | Вы ошиблись при замене корня дробным показателем: 
| |
| 5. | Нельзя отдельно интегрировать сомножители, делимое и делитель. См.  , пример 3. , пример 3.
| |
| 5. | 1. | Верно. |
| 2. | Нашли производную вместо интеграла. См. 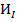 . .
| |
| 3. | Неверно. Забыли С. |
Задание №2.
| № п/п | № ответа | Пояснения |
| 1. | 1. | В  нужно вынести нужно вынести  . Вы вынесли 5, получили: . Вы вынесли 5, получили:
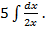 Следовательно t= Следовательно t=  , что неверно. , что неверно.
|
| 2. | Верно. | |
| 3. | Не верно. Забыли С. | |
| 2. | 1. | Верно. |
| 2. | Нужно предварительно раскрыть скобки и применить свойства 2 и 1, 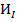 и и  . .
| |
| 3. | Нашли производную вместо интеграла. См. 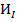 и и  . .
|
Задание №3.
| № п/п | № ответа | Пояснения |
| 1. | 1. | Не верно. Забыли С. |
| 2. | Дифференцируете вместо того, чтобы интегрировать. | |
| 3. | Верно. |
Задание №4.
| № п/п | № ответа | Пояснения |
| 1. | 1. | Верно. |
| 2. | В 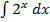 ошибочно использована ошибочно использована 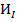 вместо вместо  . .
| |
| 3. | Не верно. Забыли С. | |
| 2. | 1. | В  вместо вместо  взяли взяли 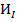 и вместо (n+1) взяли (n-1). См. и вместо (n+1) взяли (n-1). См. 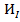 и и  . .
|
| 2. | В  нужно применить нужно применить  , а не , а не 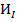 . См. . См. 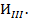
| |
| 3. | Верно. |
Задание №5.
| № п/п | № ответа | Пояснения |
| 1. | 1. | 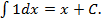 Вы его потеряли. См. свойство 3 или Вы его потеряли. См. свойство 3 или 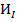 при n=0. при n=0.
|
| 2. | Ошиблись в знаке 
| |
| 3. | Верно. | |
| 4 | 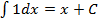 , а не 1. См. свойство 3. , а не 1. См. свойство 3.
| |
| 2. | 1. | Верно. |
| 2. | Ошибка в знаке. Должно быть -5cosx. См.  . .
| |
| 3. | 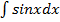 не является интегралом типа не является интегралом типа  . См. . См.  . .
| |
| 4. | 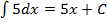 , а не 5. , а не 5.
|
Задание №6
| № п/п | № ответа | Пояснения |
| 1. | 1. | Ошибка в знаке. Должно быть 2sinx. |
| 2. | Верно. | |
| 3. | Интеграл отношения не равен отношению интегралов. Следовательно sin2x=2sinx·cosx, а затем  . А далее используйте формулу. . А далее используйте формулу.
| |
| 2. | 1. | Ошибка в знаке. Должно быть -3sinx. См.  . .
|
| 2. | Верно. |
Задание №7.
| № п/п | № ответа | Пояснения |
| 1. | 1. | Ошибка в  См. См.  . Следует разделить числитель на знаменатель. . Следует разделить числитель на знаменатель.
|
| 2. | Верно. |
Задание №8.
| № п/п | № ответа | Пояснения |
| 1. | 1. | Ошибка в знаке 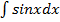 . См. . См.  . .
|
| 2. | Верно. | |
| 2. | 1. | Верно. |
| 2. | Ошибка в знаке  . См. . См.  . .
|
Задание №9.
| № п/п | № ответа | Пояснения |
| 1. | 1. | Верно. |
| 2. | Ошибка в 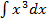 . См. . См. 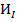 . .
| |
| 3. | Ошибка в  . См. . См.  . .
| |
| 4. | Потеряно С. |
Задание №10.
| № п/п | № ответа | Пояснения |
| 1. | 1. | Ошибка в  . См. . См.  . .
|
| 2. | Ошибка в  . См. . См.  . .
| |
| 3. | Верно. | |
| 4. | Потеряно С. |
Задание №11.
| № п/п | № ответа | Пояснения |
| 1. | 1. | Верно. |
| 2. | Вместо dx подставили просто dt, не учитывая, что при дифференцировании (5+3х) получается 3dx, следовательно, 3dx=dt, а dx=  , см. , см.  . .
| |
| 3. | Вы не проинтегрировали, а продифференцировали функцию. | |
| 4. | Потеряно С. | |
| 2. | 1. | Нашли производную вместо интеграла. |
| 2. | Потеряли коэффициент  при dt. 5dx=dt; dx= при dt. 5dx=dt; dx=  . См. . См.  . .
| |
| 3. | Верно. | |
| 4. | Потеряно С. | |
| 3. | 1. | Потеряли знак:  . См. . См.  . .
|
| 2. | Верно. | |
| 4. | 1. | Потеряли коэффициент  при dt. при dt.  . .
|
| 2. | Верно. | |
| 3. | Ошиблись в показателе, вместо  взяли -3. взяли -3.
| |
| 5. | 1. | Потерян знак d(cosx)=-sinxdx. |
| 2. | Вместо n+1 взяли n-1. | |
| 3. | Верно. | |
| 6. | 1. | Потерян знак d(3-sinx)=-cosxdx. |
| 2. | Верно. | |
| 3. | Вместо n+1 взяли n-1. | |
| 7. | 1. | Верно. |
| 2. | Потеряно С. | |
| 3. | Потерян знак. | |
| 8. | 1. | Интеграл типа 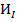 , а не , а не  , т.к. n=-5, а не n=-1. , т.к. n=-5, а не n=-1.
|
| 2. | Верно. | |
| 3. | Вместо n=-5 взяли n=5. |
Задание №12.
| № п/п | № ответа | Пояснения |
| 1. | 1. | Потеряли коэффициент  . .
|
| 2. | Ошибочно использовали 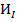 , хотя здесь n=-1, и взяли n-1 вместо n+1, что дало бы 0. , хотя здесь n=-1, и взяли n-1 вместо n+1, что дало бы 0.
| |
| 3. | Верно. | |
| 2. | 1. | Потеряли коэффициент  . .
|
| 2. | Ошибочно приняли 
| |
| 3. | Верно. | |
| 3. | 1. | Вместо  взяли взяли 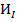 и вместо (n+1) взяли (n-1). и вместо (n+1) взяли (n-1).
|
| 2. | Верно. | |
| 3. | Нашли производную, а не интеграл. | |
| 4. | 1. | Потеряли минус. |
| 2. | Верно. | |
| 3. | Потеряли коэффициент  . .
| |
| 5. | 1. | Воспользовались 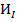 , что неверно, т.к. tgx=f(x), а не x. , что неверно, т.к. tgx=f(x), а не x.
|
| 2. | Верно. | |
| 3. | Ошибочно заменили tgx через  . .
|
Задание №13.
| № п/п | № ответа | Пояснения |
| 1. | 1. | Потерян минус в показателе степени. |
| 2. | Верно. | |
| 3. | Потерян минус перед дробью. | |
| 2. | 1. | Верно. |
| 2. | Ошибочно применили  . Этого нельзя делать, т.к. здесь показательная функция, см. . Этого нельзя делать, т.к. здесь показательная функция, см.  . .
| |
| 3. |
Задание №14.
| № п/п | № ответа | Пояснения |
| 1. | 1. | Потеряли коэффициент  , см. , см. 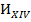 . .
|
| 2. | Верно. | |
| 3. | Потеряли минус, см. 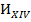 . .
| |
| 2. | 1. | Берете произведение интегралов  и и  , что неверно. , что неверно.
|
| 2. | Потеряли коэффициент  . .
| |
| 3. | Верно. | |
| 3. | 1. | Потеряли коэффициент  , см. , см. 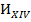 . .
|
| 2. | Верно. | |
| 3. | Потерян знак, см.  . .
|
Задание №15.
| № п/п | № ответа | Пояснения |
| 1. | 1. | Потерян коэффициент  , см. , см. 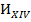 . .
|
| 2. | Верно. | |
| 3. | Пользуетесь  для n=-2, что неверно, т.к. в знаменателе не для n=-2, что неверно, т.к. в знаменателе не 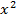 , а , а  , см. , см. 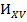 . .
| |
| 2. | 1. | Потерян коэффициент -  , см. , см. 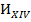 . .
|
| 2. | Верно. | |
| 3. | 1. | Неверно пользуетесь 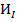 , надо применять , надо применять 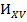 . .
|
| 2. | Верно. |
Задание №16.
| № п/п | № ответа | Пояснения |
| 1. | 1. | Потерян коэффициент  , см. , см.  . .
|
| 2. | Неверно применили  См. См.  и пример 1 к и пример 1 к  . .
| |
| 3. | Верно. | |
| 2. | 1. | Потерян коэффициент  , см. , см.  . .
|
| 2. | Потерян коэффициент  , получающийся при дифференцировании подстановки, см. , получающийся при дифференцировании подстановки, см.  . .
| |
| 3. | Верно. | |
| 3. | 1. | Верно. |
| 2. | Потерян коэффициент  , получающийся при дифференцировании подстановки, см. , получающийся при дифференцировании подстановки, см.  . .
| |
| 3. | Вместо 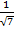 вынесли вынесли  , что неверно. , что неверно.
|
 2020-04-12
2020-04-12 129
129







