Оптимизация траектории движения носителя

 

Допущения: – аэродинамические силы отсутствуют;

                   – гравитационное поле – плоско-параллельное;

                   – планета не вращается.

 

                   Модель движения в начальной стартовой системе координат:

 

 

,

 

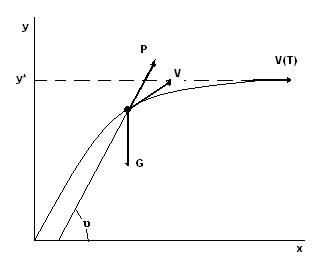
где h – высота;

       m – масса ЛА;

P – сила тяги двигателя;

J – удельный импульс;

β – секундный расход топлива;

β_m – максимально возможный расход топлива;

       g  – ускорение силы тяжести;

       g₀ – ускорение силы тяжести на поверхности планеты;

       R_P – радиус планеты. 

 

Программа управления задана в параметрической форме .

Требуется найти параметры , ,  обеспечивающие выход взлетной ступени на круговую орбиту вокруг Луны  при минимальных затратах топлива.

 

Исходные данные – взлетная ступень лунного модуля должна выйти на орбиту командного модуля Аполлон.

.

 

 

Оптимизация траектории движения носителя

 

Допущения: – аэродинамические силы отсутствуют;

                   – гравитационное поле – плоско-параллельное;

                   – планета не вращается.

 

                   Модель движения в начальной стартовой системе координат:

 

 

,

 

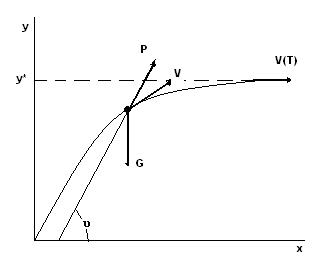
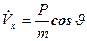
где h – высота;

       m – масса ЛА;

P – сила тяги двигателя;

J – удельный импульс;

β – секундный расход топлива;

β_m – максимально возможный расход топлива;

       g  – ускорение силы тяжести;

       g₀ – ускорение силы тяжести на поверхности планеты;

       R_P – радиус планеты. 

 

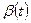Используя необходимые условия оптимального управления, найти программы управления вектором тяги  и расходом топлива, , которые обеспечат выход взлетной ступени на круговую орбиту вокруг Луны  при минимальных затратах топлива.

 

Исходные данные – взлетная ступень лунного модуля проекта Н1- Л3 должна выйти на орбиту командного модуля.