Разгон КА до параболической скорости за минимальное время

       Космический аппарат, оснащенный нерегулируемым двигателем малой тяги, стартует с начальной круговой орбиты и должен разогнаться до параболической скорости за минимально возможное время.

       Уравнения движения в безразмерных переменных имеют вид [3]:

где r – радиус; u – радиальная скорость; v – трансверсальная скорость; φ – полярный угол, λ – угол, определяющий ориентацию вектора тяги двигателя в плоскости орбиты; – начальное ускорение; V – скорость истечения реактивной струи.

       Требуется найти программу управления 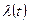, которая обеспечивает минимум времени достижения параболической скорости при заданных начальных условиях, ускорении и скорости истечения. Условие достижения параболической скорости имеет вид (при t = t_k) 

.

Примечание. Переход к безразмерным переменным осуществляется с использованием соотношений:

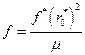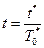, , , , где .

r – расстояние, v – скорость, f – ускорение, t - время

Звездочкой помечены размерные величины. Нижний 0 – начальное условие