Формы комплексного числа.
1. Алгебраическая 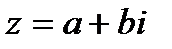
сложение: 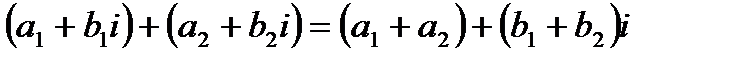
умножение: 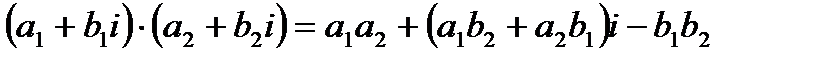
деление: 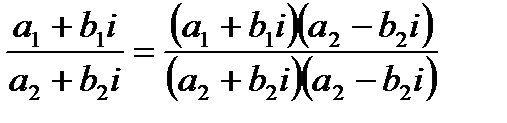
2. Тригонометрическая 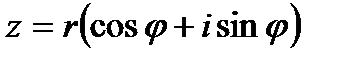
умножение: 
деление: 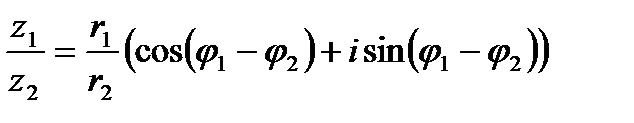
возведение в степень: 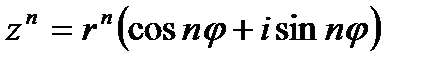
извлечение корня: 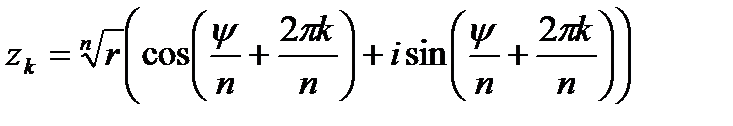 ,
, 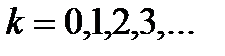
3. Показательная 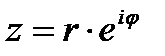
умножение: 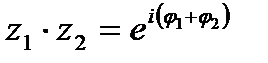
деление: 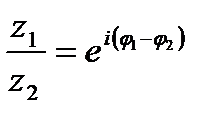
возведение в степень: 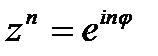
Используя методические рекомендации, выполните задания:
| 1 вариант | 2 вариант |
1. Найдите 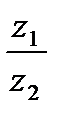 , если , если 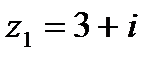 , , 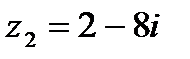
| 1. Найдите 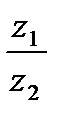 , если , если 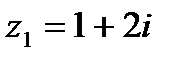 , , 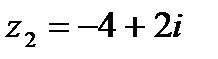
|
2. Найдите модуль к.ч. 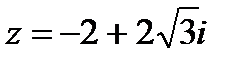
| 2. Найдите модуль к.ч. 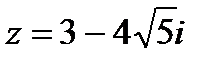
|
3. Найдите 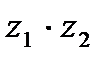 , если , если 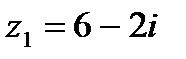 , , 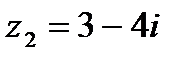
| 3. Найдите 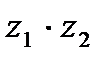 , если , если 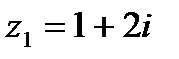 , , 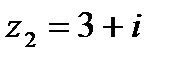
|
4. Изобразите число на комплексной плоскости 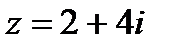
| 4. Изобразите число на комплексной плоскости 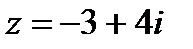
|
5. Вычислите: 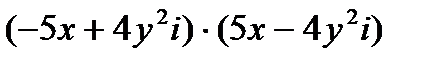
| 5. Вычислите: 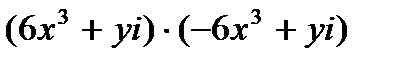
|
6. Разложите на множители:
а) 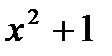 ; б) ; б) 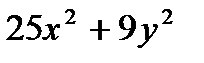
| 6. Разложите на множители:
а) 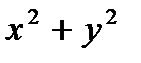 ; б) ; б) 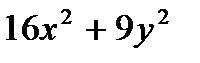
|
7. Решите уравнения:
а) 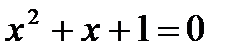 ; б) ; б) 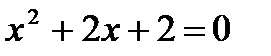
| 7. Решите уравнения:
а) 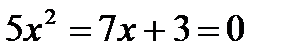 ; б) ; б) 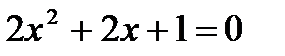
|
8. Выполнить умножение, деление и возведение в степень к.ч. 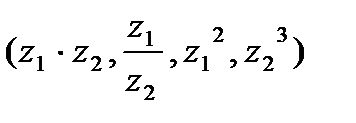 , если
а) , если
а) 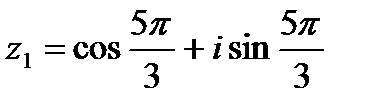 , , 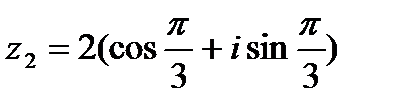 б)
б) 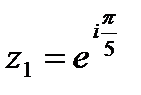 ; ; 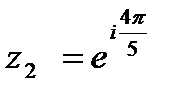
| 8. Выполните умножение, деление и возведение в степень к.ч. 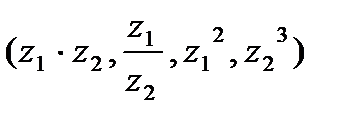 , если
а) , если
а) 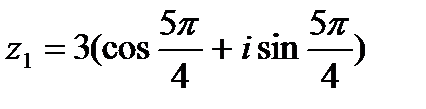 , , 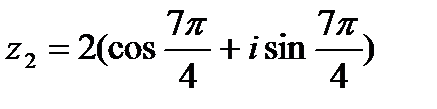 б)
б) 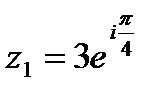 ; ; 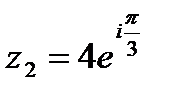
|
9. Запишите в тригонометрической и показательной форме к.ч.
а) 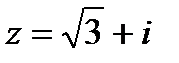 ; б) ; б) 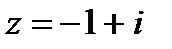
| 9. Запишите в тригонометрической и показательной форме к.ч.
а) 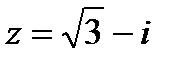 ; б) ; б) 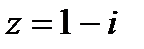
|
Тема 4. Начала математического анализа.
Самостоятельная работа №4
Способы задания и свойства числовой последовательности.
Понятие о пределе последовательности. Бесконечно убывающая геометрическая последовательность и ее сумма
Цель: Знать определение последовательности и способы ее задания. Иметь понятие о пределе последовательности, бесконечно убывающей геометрической последовательности и ее сумме.
1. Изучив тему, письменно ответьте на вопросы:
10. Сформулируйте определение последовательности.
20. Перечислите способы задания последовательности.
30. Сформулируйте определение предела последовательности.
40. Дайте понятие бесконечно убывающей геометрической прогрессии и ее сумме.
2. Выполните письменно задания: №4.38(а,г), с. 138 из [2].
Литература: 1. М.Я. Пратусевич «Алгебра и начала математического анализа, 10кл., М., «Просвещение», 2014, гл.VII, §39, §40.
2. С.М. Никольский «Алгебра и начала математического анализа, 10 кл., М., «Просвещение», 2014, §4, п.4.5.
 2020-04-12
2020-04-12 131
131








