Теоретический материал

№ п/п	Наименование фигуры	Изображение	Формула площадей полной и боковой поверхности
1	Цилиндр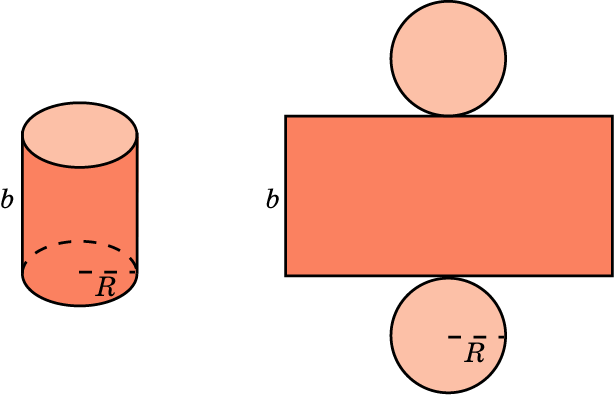
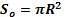
2	Конус
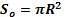
3	Сфера, шар

 

Используя методические рекомендации, решите задачи:

 

Вариант

 

1. Найдите объём правильной четырёхугольной пирамиды, сторона основания которой равна 6 см и высота 4 см.

 

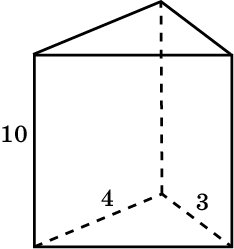
2. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 см и 4 см, высота призмы равна 10 см. Найдите объем данной призмы.

 

3. Площадь осевого сечения цилиндра равна 4 м². Найдите объем цилиндра.

4.  Высота конуса равна . образующая конуса составляет с плоскостью основания угол в . Найти объем конуса.

 

5. Площадь большого круга шара равна 3 см². Найдите  объем шара.

 

 

Вариант

1. Найдите  объём правильной треугольной пирамиды со стороной основания 6 см и высотой 1 см.

 

2. Найдите объем прямой призмы, в основании которой лежит ромб с диагоналями 6 см и 8 см и боковым ребром 10 см.

 

3. Осевое сечение цилиндра - квадрат. Площадь основания равна 1. Найдите  объем цилиндра.

 

4. Радиус основания конуса равен 3 м, высота - 4 м. Найдите площадь объем конуса.

 

5. Сечение шара плоскостью, отстоящей от центра шара на расстоянии 8 см, имеет радиус 6 см. Найдите  объем шара.

 

 

Тема 8. Интеграл и его применение.

Самостоятельная работа № 8.

Интеграл и его применение

Цель: Развитие интереса к предмету.

 

Форма самостоятельной деятельности: создание презентации по заявленной теме.

 

Работа должна соответствовать методическим рекомендациям по созданию презентации.