2020-04-12
496
1. Изучив тему, ответьте на вопросы:
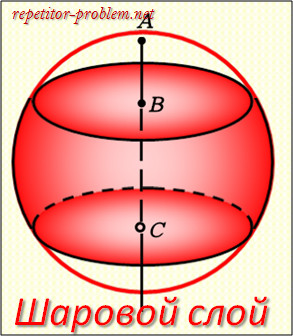
10. Дайте определение шарового сегмента.
20. Дайте определение шарового пояса.
30. Дайте определение шарового сектора.
40. Запишите формулы для нахождения площадей поверхностей частей шара.
2. Решите задачи:
10. Найдите площадь поверхности шарового сегмента, отсекаемого от шара радиуса 2, плоскостью проходящей на расстоянии 1от центра шара.
20. Шар радиуса 1 пересечен двумя параллельными плоскостями, которые делят перпендикулярный им диаметр шара в отношении 1:2:3. Определите площадь поверхности шара, заключенную между секущими плоскостями.
Литература: 1. А.Д. Александров «Геометрия»,11кл., 2014, М., «Просвещение», с. 94, с. 117.
2. Г.Н. Яковлев «Математика для техникумов. Геометрия», М., «Наука», 1987, гл. VII, §92.
Модели тел вращения
Цель: Закрепить понятие тел вращения при изготовлении моделей, используя развертки.
Форма самостоятельной деятельности: изготовление моделей тел вращения.
Методические рекомендации
Одним из способов изготовления тел вращения является способ с использованием, так называемых, развёрток.
Если модель поверхности тела вращения изготовлена из гибкого нерастяжимого материала (бумаги, тонкого картона и т. п.), то эту модель можно разрезать по образующей, отделить основание и развернуть так, чтобы она превратится в модель некоторого многоугольника плюс круг. Эту фигуру называют развёрткой поверхности тела вращения. Для получения модели тела вращения удобно сначала изготовить развёртку его поверхности. При этом необходимыми инструментами являются клей и ножницы. Модели тел вращения можно сделать, пользуясь одной разверткой, на которой будут расположены все элементы.
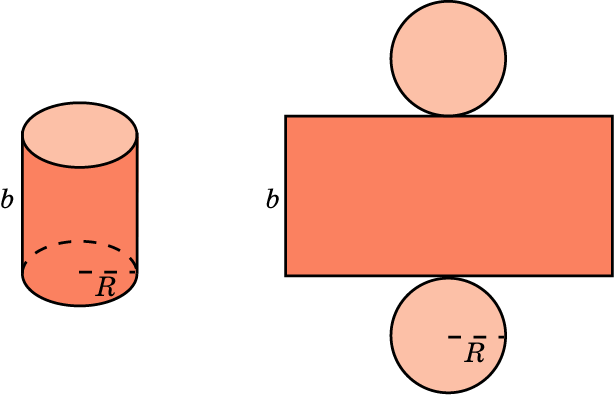
Используя развертки тел вращения, изготовьте их модели.
Решение задач по теме: «Объемы тел»
Цель: Знать формулы для нахождения объемов многогранников и тел вращения.
Методические рекомендации
Основные формулы
| № п/п | Наименование многогранника | Изображение | Площадь боковой и полной поверхности |
| 1 | Куб | 
| 
V=a3
|
| 2 | Прямоугольный параллелепипед |
| 
V=a*b*c
V=Sосн*h
|
| 3 | Призма |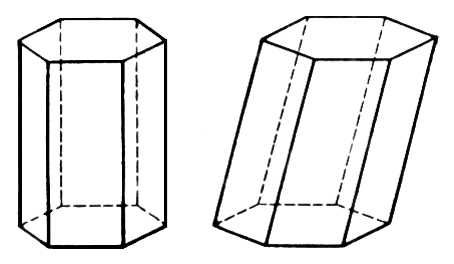 
| 
V=Sосн*h
|
| 4 | Пирамида | 
| 
V=(1/3)*Sосн*h
|
