2020-04-20
130
· EIG, CDF2RDF <http://www.exponenta.ru/soft/matlab/potemkin/book2/chapter7/eig.asp> - собственные значения и собственные векторы матрицы (Matritsaning xos son va xos vektorlari)
· BALANCE <http://www.exponenta.ru/soft/matlab/potemkin/book2/chapter7/balance.asp> - масштабирование матрицы (matritsa ko’lmamining kengligi)
· HESS <http://www.exponenta.ru/soft/matlab/potemkin/book2/chapter7/hess.asp> - приведение к форме Хессенберга (Xessenberg formasiga keltirish)
· SCHUR, RSF2CSF <http://www.exponenta.ru/soft/matlab/potemkin/book2/chapter7/schur.asp> - приведение к форме Шура (Shura formasiga keltirish
· CPLXPAIR <http://www.exponenta.ru/soft/matlab/potemkin/book2/chapter7/cplxpair.asp> - сортировка комплексно сопряженных пар (kompleks bog’langanlikni saralash)
· QZ <http://www.exponenta.ru/soft/matlab/potemkin/book2/chapter7/qz.asp> - приведение пары матриц к обобщенной форме Шура
· POLYEIG <http://www.exponenta.ru/soft/matlab/potemkin/book2/chapter7/polyeig.asp> - вычисление собственных значений матричного полинома (xos sonlarning matritsa polinomligini hisoblash)
· SVD <http://www.exponenta.ru/soft/matlab/potemkin/book2/chapter7/svd.asp> - сингулярное разложение матрицы
алгебраический программный алгоритм mathlab
4.1 Программы на языке С++
1. Поиск собственных чисел и векторов симметричной матрицы
|
|
|
/******************************************************************
Алгоритм ищет собственные пары симметричной матрицы, приводя её к трехдиагональной и используя QL/QR алгоритм.
Входные параметры:- симметричная матрица, заданная верхним или нижним треугольником. Массив с нумерацией элементов [0..N-1, 0..N-1]- размер матрицыформат храненияфлаг, сообщающий, требуются ли собственные векторы.
Если ZNeeded:
* равно 0, то собственные векторы не возвращаются
* равно 1, то собственные векторы возвращаются
Выходные параметры:- собственные числа в порядке возрастания.
Массив с нумерацией элементов [0..N-1].- если ZNeeded:
* равно 0, не модифицируется
* равно 1, содержит собственные векторы
Массив с нумерацией элементов [0..N-1, 0..N-1], при этом
собственные векторы хранятся в столбцах матрицы.
Результат:, если алгоритм сошелся, если алгоритм не сошелся (редчайший случай)
******************************************************************/
#include <stdafx.h>
#include "sevd.h"
bool smatrixevd(ap::real_2d_array a,n,zneeded,isupper,::real_1d_array& d,::real_2d_array& z)
{result;::real_1d_array tau;
ap::real_1d_array e;
ap::ap_error::make_assertion(zneeded==0||zneeded==1, "SMatrixEVD: incorrect ZNeeded");(a, n, isupper, tau, d, e);(zneeded==1)
{(a, n, isupper, tau, z);
}= smatrixtdevd(d, e, n, zneeded, z);result;
}
/******************************************************************
Obsolete 1-based subroutine
******************************************************************/
bool symmetricevd(ap::real_2d_array a,n,zneeded,isupper,::real_1d_array& d,::real_2d_array& z)
{result;::real_1d_array tau;
ap::real_1d_array e;
ap::ap_error::make_assertion(zneeded==0||zneeded==1, "SymmetricEVD: incorrect ZNeeded");
totridiagonal(a, n, isupper, tau, d, e);
if(zneeded==1)
{(a, n, isupper, tau, z);
}= tridiagonalevd(d, e, n, zneeded, z); result;
}
. Разложение Холецкого
/******************************************************************
Алгоритм осуществляет разложение Холецкого симметричной положительно определенной матрицы
|
|
|
Результатом работы алгоритма является представление матрицы A в виде A = U'*U или A = L*L'.
Входные параметры:- верхний или нижний треугольник факторизуемой матрицы.
Массив с нумерацией элементов [0..N-1, 0..N-1]- размер матрицыесли IsUpper=True, A содержит верхний треугольник симметричной матрицы, иначе A содержит нижний треугольник.
Выходные параметры:- результат факторизации. Если IsUpper=True, в верхнем треугольнике находится матрица U, такая, что A = U'*U, а элементы, лежащие ниже главной диагонали, не модифицируются. Аналогично, если IsUpper=False.
Результат:
Если матрица положительно определена, функция возвращает True.
Если матрица знаконеопределена, то функция возвращает False. При этом факторизация не может быть осуществлена.
******************************************************************/
#include <stdafx.h>
#include "cholesky.h"spdmatrixcholesky(ap::real_2d_array& a, int n, bool isupper)
{result;i;j;ajj;v;
//
// Test the input parameters.
//::ap_error::make_assertion(n>=0, "Error in SMatrixCholesky: incorrect function arguments");
// Quick return if possible= true;(n<=0)
{result;
}(isupper)
{
// Compute the Cholesky factorization A = U'*U.(j = 0; j <= n-1; j++)
{
// Compute U(J,J) and test for non-positive-definiteness.= ap::vdotproduct(a.getcolumn(j, 0, j-1), a.getcolumn(j, 0, j-1));= a(j,j)-v;(ajj<=0)
{= false;result;
}= sqrt(ajj);(j,j) = ajj;
// Compute elements J+1:N of row J.
if(j<n-1)
{(i = 0; i <= j-1; i++)
{= a(i,j);::vsub(&a(j, j+1), &a(i, j+1), ap::vlen(j+1,n-1), v);
}= 1/ajj;::vmul(&a(j, j+1), ap::vlen(j+1,n-1), v);
}
}
}
{
// Compute the Cholesky factorization A = L*L'.(j = 0; j <= n-1; j++)
{
// Compute L(J,J) and test for non-positive-definiteness.= ap::vdotproduct(&a(j, 0), &a(j, 0), ap::vlen(0,j-1));= a(j,j)-v;(ajj<=0)
{= false;result;
}= sqrt(ajj);(j,j) = ajj;
// Compute elements J+1:N of column J.
if(j<n-1)
{(i = j+1; i <= n-1; i++)
{= ap::vdotproduct(&a(i, 0), &a(j, 0), ap::vlen(0,j-1));(i,j) = a(i,j)-v;
}= 1/ajj;::vmul(a.getcolumn(j, j+1, n-1), v);
}
}
}result;
}
/******************************************************************
Obsolete 1-based subroutine.
******************************************************************/
bool choleskydecomposition(ap::real_2d_array& a, int n, bool isupper)
{result;i;j;
double ajj;v;jm1;
int jp1;
//
// Test the input parameters.
//::ap_error::make_assertion(n>=0, "Error in CholeskyDecomposition: incorrect function arguments");
//
// Quick return if possible
//= true;(n==0)
{result;
}(isupper)
{
//
// Compute the Cholesky factorization A = U'*U.
//(j = 1; j <= n; j++)
{
//
// Compute U(J,J) and test for non-positive-definiteness.
//= j-1;= ap::vdotproduct(a.getcolumn(j, 1, jm1), a.getcolumn(j, 1, jm1));= a(j,j)-v;(ajj<=0)
{= false;result;
}= sqrt(ajj);(j,j) = ajj;
//
// Compute elements J+1:N of row J.
//(j<n)
{(i = j+1; i <= n; i++)
{= j-1;= ap::vdotproduct(a.getcolumn(i, 1, jm1), a.getcolumn(j, 1, jm1));
a(j,i) = a(j,i)-v;
}= 1/ajj;= j+1;::vmul(&a(j, jp1), ap::vlen(jp1,n), v);
}
}
}
{
//
// Compute the Cholesky factorization A = L*L'.
//(j = 1; j <= n; j++)
{
//
// Compute L(J,J) and test for non-positive-definiteness.
//= j-1;= ap::vdotproduct(&a(j, 1), &a(j, 1), ap::vlen(1,jm1));= a(j,j)-v;(ajj<=0)
{= false;result;
}= sqrt(ajj);(j,j) = ajj;
//
// Compute elements J+1:N of column J.
//(j<n)
{(i = j+1; i <= n; i++)
{= j-1;= ap::vdotproduct(&a(i, 1), &a(j, 1), ap::vlen(1,jm1));(i,j) = a(i,j)-v;
}= 1/ajj;= j+1;::vmul(a.getcolumn(j, jp1, n), v);
}
}
}result;
}
М - файлы для системы MatLab
1. Метод скалярных произведений для определения наибольшего собственного значения и соответствующего ему собственного вектора.
function [L1,x1]=iter_eg(A,n,ep)
for i=1:n(i)=1;;=1;1i=1:n(i)=x1(i);;i=1:n=0;j=1:n-1
S=S+A(i,j)*x0(j);;(i)=(S+A(i,n))/L0;;=0;j=1:n-1=S+A(n,j)*x1(j);;=S+A(n,n);abs(L0-L1)<ep
break;;=L1;;
end
Результат 1:
>> A=[4,2,2; 2,5,1; 2,1,6];
>> [L1,x1]=iter_eg(A,3,0.001)
L1 =
% наибольшего собственного значения
x1 =
0.7725 1.0000 % соответствующего ему собственного вектора
>> (A-L1*eye(3))*x1'
ans =
>>
Результат 2:
>> A=[2,1,4,1;3,0,1,1;-1,2,3,4;3,1,1,1]=
1 4 1
0 1 1
2 3 4
1 1 1
>> [L1,x1]=iter_eg(A,4,0.001)=
=
0.8737 1.1341 1.0000
>> (A-L1*eye(4))*x1'=
. function [x]=holecki(A,b,n)
for i=1:n(i,1)=A(i,1);(1,i)=A(1,i)/D(1,1);(i,i)=1;;i=2:nj=2:n
if i>=j=0;k=1:j-1=S+D(i,k)*C(k,j);;(i,j)=A(i,j)-S;;i<j=0;k=1:i-1=S+D(i,k)*C(k,j);
end;(i,j)=(A(i,j)-S)/D(i,i);;;;(1)=b(1)/D(1,1);i=1:n
S=0;k=1:i-1=S+D(i,k)*y(k);
end;(i)=(b(i)-S)/D(i,i);;
x(n)=y(n);=n-1;i>=1=0;k=i+1:n=S+C(i,k)*x(k);
end;(i)=y(i)-S;=i-1;
end;
Результат:
>> A=[4,2,2; 2,5,1; 2,1,6];
>> b=[6,10,-3];
>> [x]=holecki(A,b,3)=
1.2250 1.7500 -1.2000
>> A*x'
ans =
ЗАКЛЮЧЕНИЕ
В итерационных методах собственные значения вычисляются как пределы некоторых числовых последовательностей без предварительного определения коэффициентов характеристического многочлена. Как правила, при этом одновременно находятся и собственные векторы или некоторые другие векторы, связанные с собственными простыми соотношениями. Большинство итерационных методов менее чувствительно к ошибкам округления, чем прямые, но значительно более трудоемко. Развитие этих методов и их применение в практике вычислений стало возможно лишь после создания быстродействующих машин.
|
|
|
Среди итерационных методов особое место занимает метод вращений (метод Якоби) решения полной проблемы собственных значений вещественной симметричной матрицы [21]. Основан он на построении последовательности матриц, ортогонально подобных исходной матрице и имеющих монотонно убывающие до нуля суммы квадратов всех внедиагональных элементов.
Метод вращений очень прост, легко реализуется на ЭВМ и всегда сходится. Независимо от расположения собственных значений он обладает асимптотически квадратичной сходимостью. Наличие кратных и близких собственных значений не только не замедляет сходимость метода, но, напротив, приводит к ее ускорению. Это ускорение тем значительней, чем больше близких корней. Метод вращений устойчив к влиянию ошибок округления результатов промежуточных вычислений.
Превосходные свойства этого метода послужили причиной появления ряда работ, посвященных его распространению на решение полной проблемы матриц более общего вида.
Без существенных изменений метод вращений переносится на эрмитовы и косоэрмитовы матрицы. Незначительно изменив его, можно с успехом решать полную проблему для матриц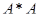 
и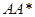 
одновременно, не вычисляя сами произведения. Но уже попытка распространить метод на общие нормальные матрицы встречает серьезные затруднения.
Нормальная матрица всегда приводится к диагональному виду с помощью унитарного преобразования. Поэтому можно было бы ожидать, что, уменьшая на каждом шаге сумму квадратов модулей внедиагональных элементов, мы приведем общую нормальную матрицу так же, как и эрмитову, к диагональной. Однако проведенные исследования показали сходимость метода вращений лишь для нормальных матриц не выше четвертого порядка.
|
|
|
Некоторые методы решения полной проблемы произвольной матрицы основаны на теореме Шура. Эта теорема дает возможность предпологать, что, подбирая подходящим образом последовательность унитарных матриц, можно с помощью подобных преобразований добиться приведения исходной матрицы к треугольной.
Описанные методы в данном реферате для определения собственных значений и собственных векторов произвольной матрицы в настоящее время являются, по-видимому, одними из наиболее эффективных.
Среди итерационных методов решения полной проблемы собственных значений значительную группу составляют степенные методы.
Полная проблема для предельной квазитреугольной матрицы решается сравнительно легко. Из теории степенных методов следует, что размеры ее диагональных клеток, как правило, не бывают большими. В частности, если все собственные значения матрицы А различны по модулю, то предельная квазитреугольная матрица будет треугольной (клетки первого порядка).
СПИСОК ЛИТЕРАТУРЫ
1. Ф. Р. Гантмахер. Теория матриц. - М. <C:\wiki\РњРѕСЃРєРІР°>: Наука <C:\wiki\Наука_(издательство)>, 1967 <C:\wiki\1967_РіРѕРґ>. - 576 с.
. Уилкинсон Д.Х. Алгебраическая проблема собственных значений. - М.: Наука, -1970. -С.564с.
3. Д.К.Фаддеев, В.Н.Фаддеева. Вычислительные методы линейной алгебры. М.: Наука, -1963.
4. В.В.Воеводин. Численные методы алгебры (теория и алгорифмы). М.: Наука, -1966.
5. Л.Коллатц. Задачи на собственные значения. М.: Наука, -1968.
6. К.Ю.Богачев. Методы решения линейных систем и нахождения собственных значений. М. -1998.
7. Белов С.А., Золотых Н.Ю. Численные методы линейное алгебры. Лабораторный практикум. - нижний Новгород: Изд-во Нижегородского госуниверситета им Н.И.Лобачевского, 2005. - 264 с.
. Воеводин В.В., Решение полной проблемы собственных значений обобщенным методом вращений, Вычислительные методы и программирование, 3, 1965, 89 - 105.
9. Воеводин В.В., Решение полной проблемы собственных значений степенными методами, Вычислительные методы и программирование
. Тыртышников. Мачричный анализ и линейная алгебра. М. 2005.
. В.И.Киреев, А.В.Пантелеев. Численные методы в примерах и задачах. М.:Высшая школа, - 2006.
12. О.В.Мантуров, Ю.К.Солнцев, Ю.И.Соркин, Н.Г.Федин. Математика терминлари изоҳли луғати. Т.:Ўқитувчи, 1974 й.
13. Потемкин В.Г. Система MATLAB. Справочное пособие.- М., ДИАЛОГМИФИ, 1997. -370с.
14. Н.Б.Культин. С/C++ в задачах и примерах. - СПб.:БХВ - Петербург
