Математичні моделі процесу електрохімічного травлення голки

 

На рис. 3 зображено профілі голки в різні моменти часу. З малюнка маємо: [5]

 

, .

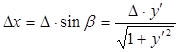Координати кожної точки кривої перетворяться по наступному закону:

 

.

 

 

Для опису процесу електрохімічного травлення можна користуватися різними моделями. Розглянемо деякі з них.

Система рівнянь в приватних похідних від двох змінних.

Залежність зміщення точки пропорційно часу протікання реакції висловимо рівністю Δ = k Δt. На швидкість реакції, яка задається коефіцієнтом k поки не накладається ніяких обмежень.

Тоді отримаємо систему рівнянь, що описує процес травлення для будь-якого коефіцієнта швидкості розчинності: [4]

 

.

 

У диференціальної формі

 

 

1. Система рівнянь в приватних похідних від однієї змінної. [5]

Припустимо, що в будь-який момент часу голка є симетричною щодо своєї осі.

Позначимо її профіль у вигляді функції y = f (x, t) (змінна x на-спрямована вздовж осі). Беручи до уваги, що , отримаємо

 

.

 

Після перетворень,, де φ (x) - початкова форма голки.

. Облік залежності швидкості травлення від кривизни профілю. [4]

Відомо, що швидкість реакції відрізняється від середньої тим більше, чим більшу кривизну має поверхню, причому на опуклих ділянках вона більше, на увігнутих - менше.

 

Рис 1.4

Рис. 1.5.

 

У разі рівної поверхні (на рис. 1.4. кривизна дорівнює нулю) атоми, розташовані на ній відчувають приблизно однаковий вплив (притягання) як атомів самого речовини, так і речовини розчинника. Однак відносини між ними різко змінюється на нерівних ділянках (на рис. 1.5. кривизна негативна), так як ступінь впливу пропорційна відношенню площ частин сфери, укладеної всередині тілесних кутів речовини і розчинника.

Характер зміни цього співвідношення можна уявити собі наступним чином. Якщо позначити через ε ставлення кута при вершині нерівності до розгорнутому повного кутку (π), то беручи до уваги, що площа поверхні всередині тілесного кута пропорційна квадрату його розчину, отримаємо, що відношення площ можна представити відношенням . Графік цієї залежності наведено на

 

Рис. 1.6.

 

Безпосередньо з малюнка слідує, що швидкість розчинення швидко збільшується при зменшенні кута ε (гостра опуклість) і зменшується до 0 при його збільшенні (глибока западина).

Залежність швидкості розчинення від кривизни можна врахувати за допомогою формули k (x) = w (K (x)), в якій K (x) - кривизна поверхні в точці. Функція w враховує знак кривизни з урахуванням того, що опуклі частини поверхні труяться швидше, увігнуті - повільніше. Якщо поверхня голки задається у вигляді функції f (x, t), то

 

.

 

У підсумку рівняння для зміни поверхні голки в процесі травлення приймає вигляд:

 

,

 

з початковою умовою у вигляді контуру дроту φ (x): .

 

Стаціонарні рішення

 

Розглянемо випадок, коли в процесі травлення голки її форма (f (x, t)) не змінюється. Для цього досить, наприклад, щоб рішення задовольняло рівності f (x, t) = g (x - сt). Геометрично воно означає, що кінець голки рухається (розчиняючись) уздовж осі з постійною швидкістю a. Дріт, з якої виходить голка, передбачається нескінченною. [5] Якщо швидкість розчинності k постійна для всіх точок поверхні, то стаціонарне рішення має задовольняти рівнянню

,

 

рішення якого  дає конус.

Недолік розглянутої моделі полягає в тому, що вістря конуса має нульовий радіус заокруглення і, з цієї причини не може бути взято в якості наближення до результату процесу травлення. Більш істотно, що при цьому не виходить оцінки на радіус заокруглення голки ні знизу ні зверху.

Для того, щоб врахувати ту обставину, що ділянки з великою кривизною труяться швидше, виберемо коефіцієнт k пропорційним кривизні. Будемо також вважати, що в будь-який момент часу голка є опуклою. У цьому випадку функція w повинна бути негативною. Приймемо її рівною константі. Розглянемо плюси і мінуси такого підходу: [5]

1. При нульовій кривизні швидкість травлення стає нескінченною. Тому важко очікувати, що в якості вирішення вийдуть фігури з надмалим радіусом заокруглення. Отримана оцінка радіуса заокруглення буде оцінкою зверху.

. При малій кривизні, тобто для плоских ділянок, швидкість травлення наближається до нульової, що не відповідає дійсності. Протиріччя з реальністю можна зменшити, якщо припустити, що в процесі травлення голка запихається в розчин.

Можна також взяти до уваги, що в процесі реакції утворюються бульбашки газу, які, піднімаючись вгору, перешкоджає надходженню лугу до голки. Цей процес призводить до істотного уповільнення реакції у верхніх шарах. [5] Рівняння утворить контуру поверхні голки прийме вигляд:

 

.

Після перетворень приходимо до рівняння

 

.

 

Роблячи заміну , знижуємо порядок рівняння

 

 

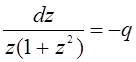
і приходимо до розв’язку

 

.

 

Звідки випливає, що

 

.

 

З урахуванням розглянутого випадку, в якому приймається, що при нульовому радіусі заокруглення швидкість травлення голки нескінченна, отримуємо умову . Звідки C₁ = 1. Крім того, не обмежуючи спільності розгляду, можна прийняти g (0) = 0. У цьому випадку, C₂ = 0. Графік функції 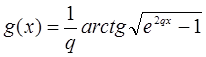 зображений на рис. 1.7. Він показує форму голки в стаціонарному випадку.

Факт існування стаціонарного рішення говорить про наявність таких умов, при яких форма голки не змінюється в процесі розчинення. Питання про те, чи буде процес формування голки з дроту (що має форму циліндра) сходитися до стаціонарної формі, вимагає окремого розгляду.

 

Рис. 1.7.

 

На кінці голки (при )

 

.

 

Чим менше коефіцієнт при , тим гостріше голка. Відповідно до отриманої формулою в стаціонарному вирішенні радіус заокруглення кінця залежить тільки від діаметра дроту. Записавши це рівність у вигляді

 

,

 

знаходимо, що радіус заокруглення дорівнює , що означає, що малий радіус заокруглення може бути отриманий при малому діаметрі дроту. Це пояснюється зробленим припущенням про те, що при нульовому радіусі заокруглення швидкість травлення нескінченна. Покажемо це.

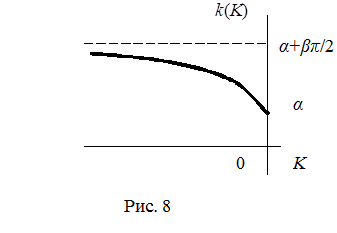
Для того, щоб врахувати особливості розчинення при малих і великих значеннях кривизни припустимо, що швидкість розчинення дається формулою:

.

 

Коефіцієнти α і β позитивні, кривизна K (x) негативна (оскільки функція g (x) передбачається опуклою). Графік залежності наведено на рис. 1.8. Вибираючи підходящими коефіцієнти, можна отримати будь-яке співвідношення між швидкостями розчинності при малих і великих величинах кривизни. У підсумку приходимо до рівняння [5]

 

.

 

 

Воно забороняє рішення у вигляді стрижня, так як не існує рішення для α ≠ 0 з асимптотичними умовам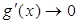и ,  при 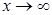. Разом з тим, можливе вирішення типу конуса (рис. 1.9.): ,  при .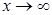

Прийнявши розчин конуса за γ (), отримаємо для нього рівняння: , яке має рішення для всіх значень α. При цьому виявляється, що швидкість розчинення голки в стаціонарному процесі залежить від тільки кута розчину конуса:

Рис. 1.9.

 

.

 

Для того, щоб знайти радіус заокруглення голки розглянемо рішення, в якому  велике. У цьому випадку рівняння спрощується:

 

.

 

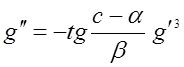Вирішуючи його, отримаємо:

 

 і  = .

 

Безпосередньо з формули рішення випливає, що величина радіуса заокруглення голки явно залежить від розчину конуса. Нагоди, малого радіуса заокруглення відповідають великі значення знаменника. Для того, щоб задовольнити цій умові достатньо взяти γ << 1. Тоді формула рішення спрощується:

.

 

Ця формула дозволяє зробити висновок про те, що за рахунок вибору заготовки у вигляді конуса з малим розчином можна забезпечити отримання голки зі як завгодно малим радіусом заокруглення.

 

Розділ 2. Використання електрохімічної обробки для заточування голок тунельного ефекту

 

Опис приладу

 

Для демонстрації заточування голки за допомогою явища електролізу складають електричне коло за схемою, поданою на малюнку 2.1. [10]

 

Мал. 2.1. 1 - електролітична ванна; 2 - розчин NaCl; 3 - катод (к); 4 - голкотримач; 5 - анод; А - амперметр; К - ключ.

 

В якості електролітичної ванни, в нас була звичайна пластикова посудина з 5-відсотковим розчином NaCl. Катодом в нас виступав мідний електрод, а анодом - голка. Джерелом струму в нас виступав випрямляч напруги ВС-24.