Точное значение массы стержня вычисляется по формуле

.

Далее вводится понятие интеграла, как предела суммы.

Задача о перемещении точки.

При введении определенного интеграла, в качестве задачи, приводящей к данному понятию, наиболее рациональным и простым для понимания учащимися является рассмотрение задачи о перемещении точки, т. к. с обратной задачей школьники уже встречались при изучении применения производной в физике.

Между положением (координатной) точки и её скоростью есть известная связь, лежащая в основе математического анализа: скорость является производной от координаты по времени. Сама операция нахождения производной называется дифференцированием. Обратная задача – нахождение положения точки по её скорости – решается с помощью другой математической операции, называемой интегрированием.

Задача. Пусть по прямой движется материальная точка. Зависимость скорости от времени выражается формулой v=v(t). Найти перемещение точки за промежуток времени [ a; b ].

Если бы движение было равномерным, то задача решалась бы очень просто: s=vt, т. е. s=v(b-a). Для неравномерного движения разобьём промежуток времени [ a; b ] на n равных частей. Рассмотрим промежуток времени [ t_k-1; t_k ] и будем считать, что в этот промежуток времени скорость была постоянной, такой как в момент времени t_k: v=v(t_k). Перемещение точки за промежуток времени [ t_k-1; t_k ] приближенно можно представить как произведение v(t_k) Δ t_k. Найдем приближенное значение перемещения s:

s ≈ S_n,

где S_k=v(t₁) Δ t₁+…+v(t_k) Δ t _k.

Точное значение перемещения вычисляется по формуле

.

Далее вводится понятие интеграла, как предела суммы. [10]

Введение понятия интеграла как приращения первообразной ни в одном из рассмотренных учебников не используется, примеры данного метода введения будут приведены в следующей главе.

 

Различные методы изучения приложений интеграла в

Физике.

Авторы различных учебников по–разному выводят формулы при изучении приложений интеграла. Рассмотрим несколько различных методов получения (вывода) формул. I. Составление интегральных сумм. Масса стержня переменной плотности. Будем считать, что отрезок [ a; b ] оси Ох имеет массу с переменной линейной плотностью ρ(х) 0, где ρ(х) – непрерывная на отрезке [ a; b ] функция. Общая масса этого отрезка ,где a=x₀<x₁<…<x_n=b, Δ x_i =x_i+1-x_i. Аналогично можно вывести формулы для нахождения работы силы, работы электрического заряда, давления жидкости на стенку, центра тяжести системы материальных точек. [11] Центр масс. При нахождении центра масс пользуются следующими правилами:Координата  центра масс системы материальных точек А₁, А₂,…, А_n с массами m₁, m₂,…, m_n, расположенных на прямой в точках с координатами x₁, x₂,…, x_n, находится по формуле .2)     При вычислении координаты центра масс можно любую часть фигуры заменить на материальную точку, поместив её в центр масс этой части, и приписать ей массу, равную массе рассматриваемой части фигуры.Пусть вдоль стержня – отрезка [ a; b ] оси Ох – распределена масса плотностью ρ(х), где ρ(х) – непрерывная функция. Покажем, что координата центра масс  равна 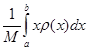.Разобьем отрезок [ a; b ] на n равных частей точками a=x₀<x₁<…<x_n=b. На каждом из n этих отрезков плотность можно считать при больших n постоянной и примерно равной ρ(x_k-1) на k -м отрезке (в силу непрерывности ρ(х)). Тогда масса k -отрезка примерно равна , а масса всего стержня равна . Считая каждый из n маленьких отрезков материальной точкой массы m_k, помещенной в точке x_k-1, получим, что координата центра масс приближенно находится так:

.

Теперь осталось заметить, что при  числитель стремится к интегралу , а знаменатель (выражающий массу всего стержня) – к интегралу . [8]

Аналогично можно вывести формулу для нахождения работы силы.