2020-04-20
353
Последовательность прямоугольных видеоимпульсов. Рассмотрим спектр сигнала, изображенного на рис. 1.3. Такой сигнал часто используется в различных радиотехнических приложениях, а его модель — в теоретической радиотехнике.
Аналитическое представление сигнала на интервале Т (представительный сигнал на периоде):
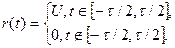(1.24)
Введено обозначение длительности прямоугольного импульса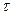 
.Воспользуемся комплексной формой ряда Фурье (1.21):
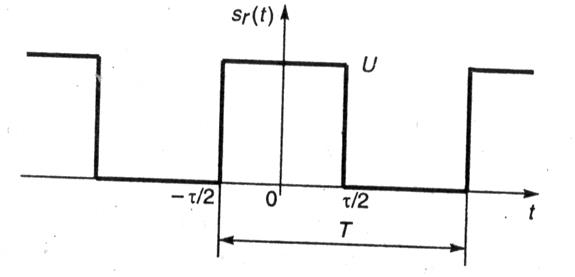
Рис. 1.3. Последовательность прямоугольных видеоимпульсов
(1.25)
Вместо пределов интегрирования 0 и Т использовано обозначение (Т), указывающее на необходимость интегрирования по интервалу Т (см. § 1.2, замечание 1). Удобные для вычислений пределы интегрирования появляются при подстановке в подынтегральное выражение конкретного r(t).
Так как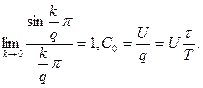 
Численно 
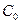и остальные коэффициенты Ск определяются по формуле (1.25) при задании конкретного значения отношения 
, которое называют скважностью последовательности. Коэффициенты с номерами k = q, 2q, 3q,... равны 0. Анализируя поведение амплитудного спектра, удобно рассматривать функцию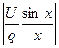 
(заменяя дискретный аргумент синуса 
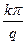непрерывным аргументом х), как
|
|
|
огибающую дискретного амплитудного спектра 
. Огибающая (пунктирная линия) и спектр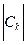 
для q = 6 и U = 1 приведены на рис. 1.4.
При q = 2 коэффициенты разложения последовательности прямоугольных видеоимпульсов в ряд Фурье в комплексной форме приобретают значения.
Рис. 1.4. Амплитудный спектр последовательности прямоугольных видеоимпульсов (q = 6)
(1.26)
Так что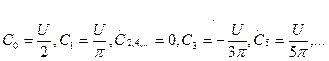 
Разложение представляется следующим образом:
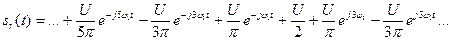(1.27)
Каждая пара составляющих вида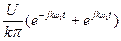 
преобразуется по формуле Эйлера:
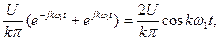
и ряд (1.27) может быть записан в виде
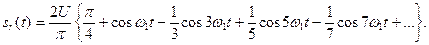(1.28)
Так как последовательность на рис. 1.3 является четным сигналом, представление (1.28) можно рассматривать и как ряд Фурье в форме (1.16) с коэффициентами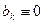 
, и как ряд Фурье в форме (1.19). В последнем случае фазовый спектр 
«обеспечивает» соответствующие знаки перед гармониками разложения, поэтому принимают 
так что
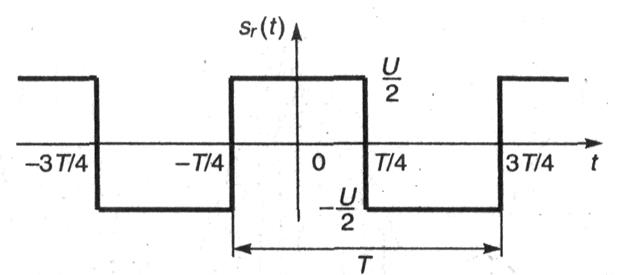
Рис. 1.5. Меандр
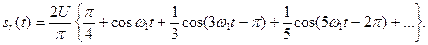
В качестве упражнения читателю рекомендуется самостоятельно найти разложение в ряд Фурье для сигнала, изображенного на рис. 1.5. Такой сигнал также часто используется в различных радиотехнических приложениях и называется меандром.
|
|
|
Аналитически формирующий меандр sr(t) представительный
сигнал последовательности r(t) на интервале Т может быть записан так:
Легко видеть, что рассмотренная последовательность прямоугольных видеоимпульсов получается суммированием меандра с постоянной составляющей U/2, которой обязан своим появлением в разложении (1.27) член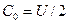 
.
Заметим, что значения коэффициентов разложения последовательности прямоугольных видеоимпульсов (при q = 2) и меандра убывают по закону 1/k.
Последовательность треугольных видеоимпульсов. Рассмотрим периодический сигнал, состоящий из треугольных видеоимпульсов (рис. 1.6). Аналитическое выражение для импульса последовательности:
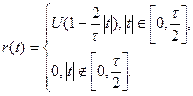(1.29)
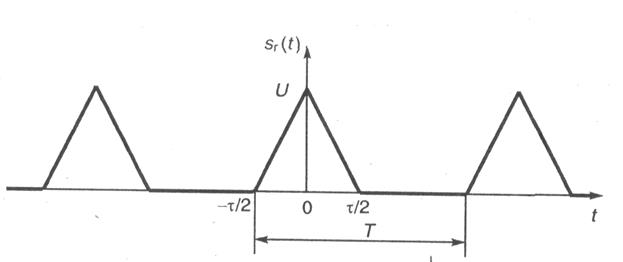
Рис. 1.6. Последовательность треугольных видеоимпульсов
Вновь обратившись к ряду Фурье в комплексной форме (1.21), выпишем выражение для коэффициентов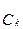 
:
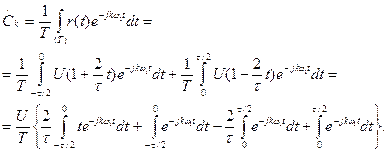
После вычисления интегралов и несложных, но громоздких выкладок (которые читателю предлагается проделать самостоятельно), получим
(1.30)
Положив q — 1, чтобы длительность треугольного видеоимпульса (1.29) «по основанию» 
совпадала с периодом последовательности Т, получим выражение для коэффициентов ряда (1.21):
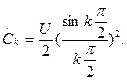
Обнаруживается связь между спектрами сигналов (1.24) и (1.29); но значения коэффициентов разложения последовательности треугольных видеоимпульсов (1.29), определенных, по аналогии с (1.28), суммированием соответствующих пар составляющих ряда Фурье в комплексной форме,
убывают по закону 1/к2, т. е. существенно быстрее коэффициентов разложения (1.28). Это связано с формой треугольного видеоимпульса: в нем отсутствуют «скачки» или разрывы 1 -го рода.
